- Författare Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:14.
- Senast ändrad 2025-01-23 12:47.
Subtraktion är helt enkelt att subtrahera ett tal från ett annat. Det är lätt att subtrahera ett helt tal från ett annat, men subtraktion kan vara knepig om du subtraherar bråk eller decimaler. När du väl förstår subtraktion kommer du att kunna använda mer komplexa matematiska begrepp och lättare kunna lägga till, multiplicera och dela tal.
Steg
Metod 1 av 6: subtrahera stora heltal genom att låna

Steg 1. Skriv ner ett stort antal
Till exempel vill du lösa 32 - 17. Skriv ner 32 först.

Steg 2. Skriv det mindre numret precis under det
Se till att du placerar tiotalet och enorna i rätt kolumner, så att 3 av 32 är direkt över 1 av 17 och 2 av 32 är direkt över 7 av 17.
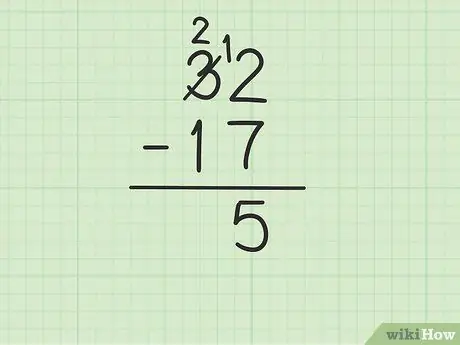
Steg 3. Dra det högsta numret i enhetskolumnen från talet längst ner
Detta kan dock bli komplicerat om det nedre talet är större än det högsta. I det här fallet är 7 större än 2. Här är vad du behöver göra:
- Du måste låna från nummer 3 av 32 (även känd som gruppering), för att göra 2 till 12.
- Korsa siffran 3 av 32 och ersätt den med siffran 2, medan siffran 2 blir 12.
- Nu kan du subtrahera 12 - 7, vilket är lika med 5. Skriv 5 under de två siffrorna du subtraherar så att de finns i kolumnen enheter på den nya raden.
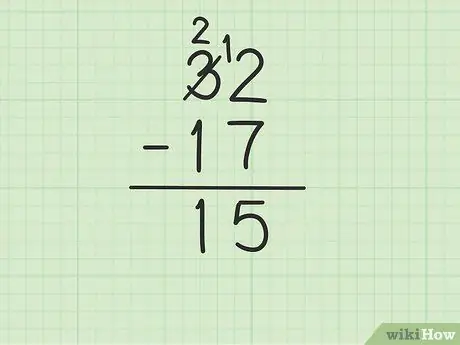
Steg 4. Subtrahera det översta talet i kolumnen tio från det nedre talet
Kom ihåg att 3 har blivit 2. Dra nu 1 från 17 från 2 ovan för att få (2-1) 1. Skriv 1 nedan, i tio-kolumnen, till vänster om 5 i kolumnen enheter. Du skriver 15. Det vill säga 32 - 17 = 15.
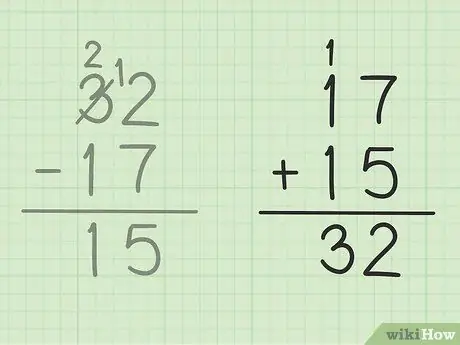
Steg 5. Kontrollera ditt arbete
Om du vill se till att du har subtraherat två siffror korrekt är det bara att lägga till ditt svar med det mindre talet för att göra ett stort tal. I detta problem måste du lägga till ditt svar, 15 till det mindre antalet subtraktion, 17. 15 + 17 = 32, så att ditt svar är korrekt. Säker!
Metod 2 av 6: subtrahera små heltal
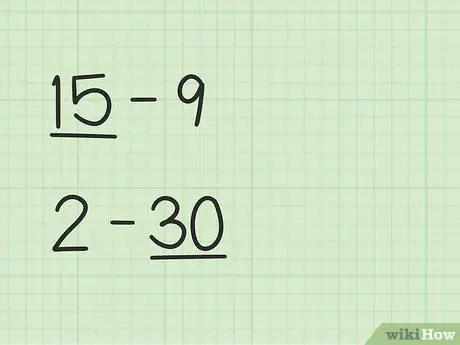
Steg 1. Hitta det större numret
Problem som 15 -9 kommer att ha ett annat sätt än 2 -30.
- I frågor 15 - 9 är det första talet, 15, större än det andra talet, 9.
- I frågor 2 - 30 är det andra talet, 30, större än det första talet, 2.
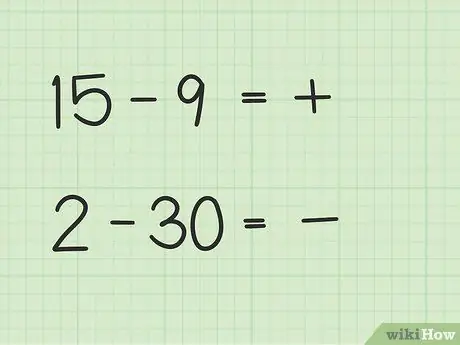
Steg 2. Bestäm om ditt svar kommer att vara positivt eller negativt
Om det första numret är större är svaret positivt. Om det andra talet är större är svaret negativt.
- I den första frågan, 15 - 9, är ditt svar positivt eftersom det första talet är större än det andra talet.
- I den andra frågan, 2 - 30, är ditt svar negativt eftersom det andra talet är större än det första talet.
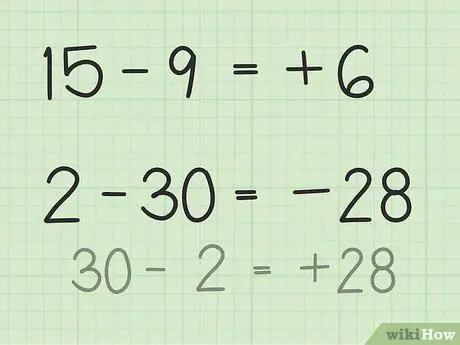
Steg 3. Hitta skillnaden mellan två nummer
För att subtrahera två tal måste du föreställa dig skillnaden mellan de två talen och beräkna siffrorna mellan dem.
- För frågor 15 - 9, föreställ dig en bunt med 15 pokerchips. Kasta 9 marker och bara 6. Så, 15 - 9 = 6. Du kan också tänka dig en sifferrad. Tänk på siffrorna från 1 till 15, släng sedan eller returnera 9 enheter så att du får 6.
- För frågor 2 - 30 är det enklaste sättet att lösa detta att invertera talet och göra resultatet negativt efter att ha subtraherat. Så, 30 - 2 = 28 så 28 och 30 har en skillnad på 2. Gör nu resultatet negativt eftersom du redan har bestämt att svaret är negativt eftersom det andra talet är större än det första talet. Så, 2 -30 = -28.
Metod 3 av 6: Subtrahera decimaler
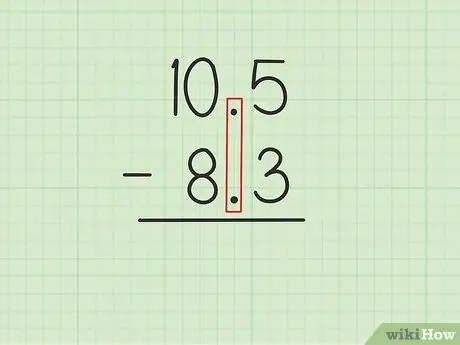
Steg 1. Skriv det större talet över det mindre talet med decimalerna i linje
Antag att du vill lösa följande problem: 10, 5 - 8, 3. Skriv 10, 5 över 8, 3 så att decimalerna i de två talen är parallella., 5 av 10, 5 måste vara direkt ovanför, 3 av 8, 3 och 0 av 10, 5 måste vara över 8 av 8, 3.
Om du har ett problem eftersom de två talen inte har samma siffra efter decimalpunkten, skriv 0 i tomrummet tills summan av siffrorna är densamma. Till exempel är problemet 5, 32 - 4, 2, du kan skriva det som 5, 32 - 4, 2 0. Detta ändrar inte värdet på det andra numret, men gör det lättare att subtrahera de två talen.

Steg 2. Subtrahera det översta talet i kolumnen tio från talet nedan
I det här fallet måste du subtrahera 3 från 5. 5 - 3 = 2, så du måste skriva 2 under 3 av 8, 3.
Se till att du sätter en decimal i svaret, så att det är skrivet, 2

Steg 3. Subtrahera numret ovanför kolumnen enheter från talet nedanför det
Du måste subtrahera 8 från 0. Låna 1 från tiotalet för att ändra 0 till 10 och subtrahera 10 - 8 för att få 2. Du kan också räkna 10 - 8 utan att låna eftersom det inte finns några nummer i den andra tiokolumnen. Skriv svaret under 8, till vänster om decimalpunkten.

Steg 4. Skriv ner ditt slutresultat
Ditt slutliga resultat är 2, 2.

Steg 5. Kontrollera ditt arbete
Om du vill se till att din decimal subtrahering är korrekt är det bara att lägga till ditt svar med det mindre talet för att göra det större talet. 2, 2 + 8, 3 = 10, 5, så du är klar.
Metod 4 av 6: Subtrahera fraktioner

Steg 1. Rikta in fraktionens nämnare och täljare
Antag att du vill lösa problem 13/10 - 3/5. Skriv problemet så att de två räknarna, 13 och 3 och de två nämnare, 10 och 5 är motsatta varandra. Dessa två tal separeras med ett subtraktionstecken. Detta hjälper dig att visualisera problemet och lösa det lättare.

Steg 2. Hitta den minst gemensamma nämnaren
Den minst gemensamma nämnaren är det minsta tal som kan delas med två tal. I det här exemplet måste du hitta den minsta gemensamma nämnaren som är delbar med 10 och 5. Du kommer att upptäcka att 10 är den minsta gemensamma nämnaren för båda talen eftersom 10 är delbart med 10 och 5.
Observera att den minst gemensamma nämnaren av två tal inte alltid är ett av dem. Till exempel är den minsta gemensamma nämnaren för 3 och 2 6 eftersom 6 är det minsta tal som kan delas med två tal
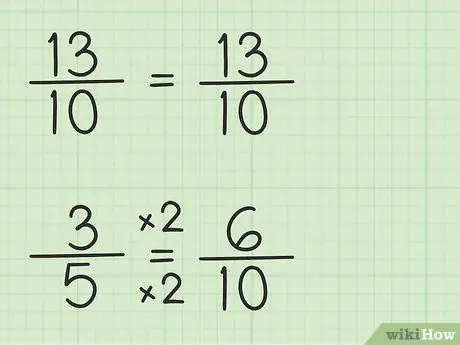
Steg 3. Skriv ner fraktionerna med samma nämnare
Bråk 13/10 kan skrivas på samma sätt eftersom nämnaren är 10, den minsta gemensamma nämnaren, som är 10, gånger 1. Dock måste bråkdelen 3/5 skrivas om eftersom nämnaren är 5, den minsta gemensamma nämnaren, som är 10, gånger 2. Så fraktionen 3/5 måste multipliceras med 2/2 för att göra nämnaren 10, så 3/5 x 2/2 = 6/10. Du har hittat motsvarande fraktion. 3/5 motsvarar 6/10 även om 6/10 låter dig subtrahera det första talet, 13/10.
Skriv en ny fråga så här: 13/10 - 6/10
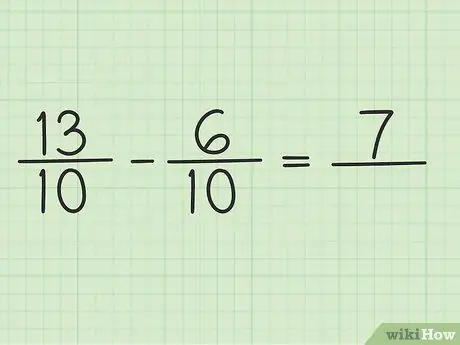
Steg 4. Subtrahera täljaren till två nummer
Bara subtrahera 13 - 6 så blir resultatet 7. Du kan inte ändra nämnaren för fraktionen.
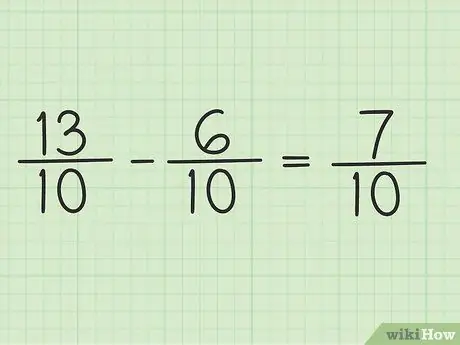
Steg 5. Skriv den nya täljaren över samma nämnare för att få det slutliga resultatet
Den nya täljaren är 7. Båda fraktionerna har nämnaren 10. Ditt slutliga resultat är 7/10.
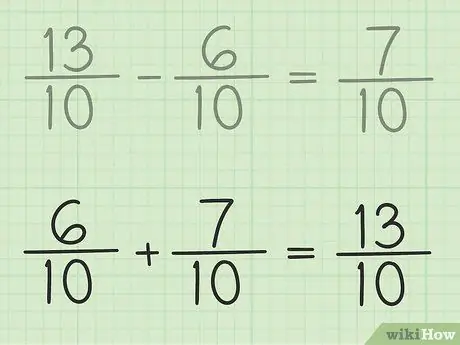
Steg 6. Kontrollera ditt arbete
Om du vill se till att du subtraherar fraktionen korrekt lägger du bara till ditt svar och den mindre fraktionen så att resultatet blir en större bråkdel. 7/10 + 6/10 = 13/10. Det är avslutat.
Metod 5 av 6: subtrahera bråk från heltal

Steg 1. Skriv ner problemet
Anta till exempel att du vill lösa följande problem: 5 -. Skriv ner det.
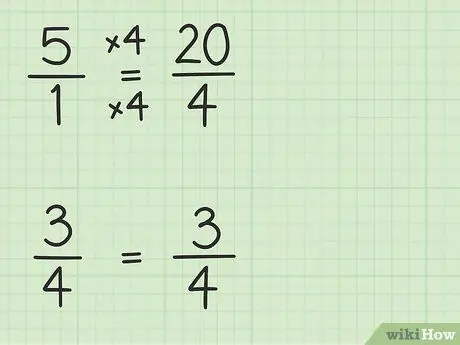
Steg 2. Konvertera heltal till bråk som har samma nämnare som andra bråk
Du kommer att konvertera 5 till en bråkdel med en nämnare på 4 för att kunna subtrahera två tal. Så du måste tänka på 5 som en bråkdel av 5/1. Sedan kan du multiplicera den nya bråkets täljare och nämnare med 4 för att göra de två siffrans nämnare desamma. Så 5/1 x 4/4 = 20/4. Denna bråkdel är lika med 5, men låter dig subtrahera två tal.
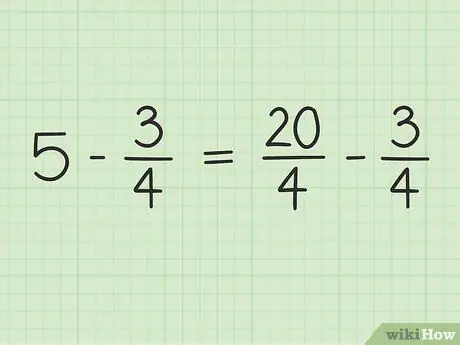
Steg 3. Skriv om problemet
Det nya problemet kan skrivas så här: 20/4 - 3/4.
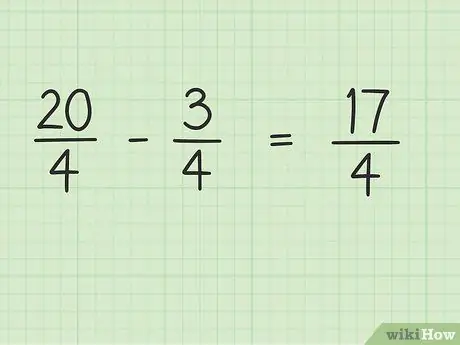
Steg 4. Subtrahera täljaren för fraktionen medan nämnaren förblir densamma
Nu, bara subtrahera 20 med 3 för att få det slutliga resultatet. 20 - 3 = 17, så 17 är den nya räknaren. Du kan lämna nämnaren densamma.
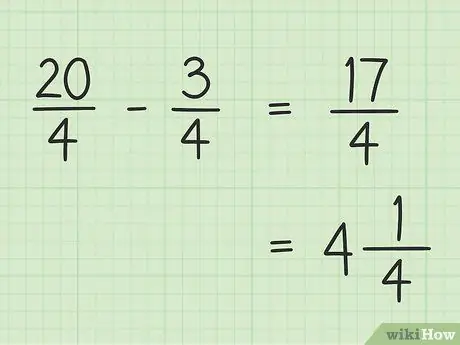
Steg 5. Skriv ner ditt slutresultat
Ditt slutliga resultat är 17/4. Om du vill skriva det som ett blandat tal, dela 17 med 4 så att resultatet blir 4 och resten är 1, så att din sista 17/4 är lika med 4.
Metod 6 av 6: Subtrahera variabler
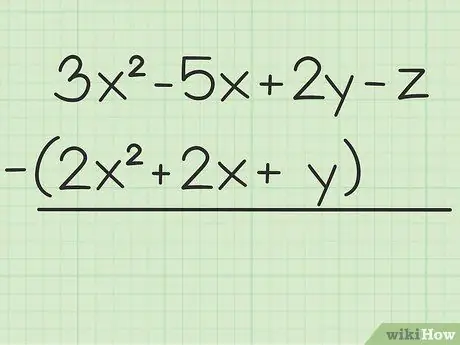
Steg 1. Skriv ner problemet du vill lösa
Till exempel följande fråga: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Skriv den första variabeln över den andra.
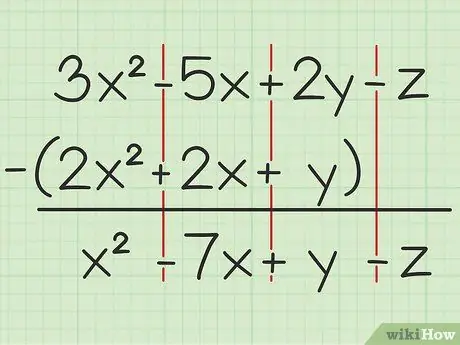
Steg 2. Subtrahera samma variabler
Om du stöter på en variabel kan du bara lägga till eller subtrahera samma variabel och som är skriven med samma kvadratgrad. Det betyder att du kan subtrahera 4x2 från 7x2, men kan inte subtrahera 4x från 4y. Så du kan dela upp problemet så här:
- 3x2 - 2x2 = x2
- -5x -2x = -7x
- 2y - y = y
- -z -0 = -z
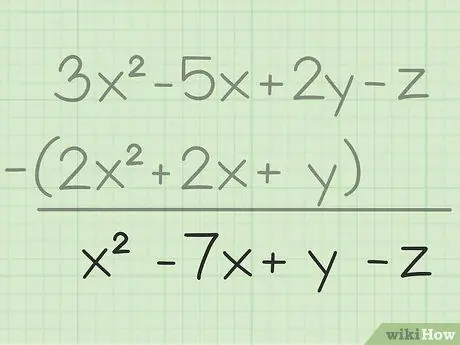
Steg 3. Skriv ner ditt slutresultat
Du har subtraherat alla samma variabler, allt du behöver göra är att skriva ditt slutresultat som innehåller alla variabler du har subtraherat. Här är slutresultatet:






