- Författare Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:40.
- Senast ändrad 2025-01-23 12:48.
Kvadratroten i ett tal är lätt att hitta om svaret är ett heltal. Om svaret inte är ett heltal finns det en serie processer du kan följa för att få kvadratroten, även om du inte använder en miniräknare. För det måste du förstå grunderna för multiplikation, addition och division.
Steg
Metod 1 av 3: Hitta kvadratroten på ett heltal
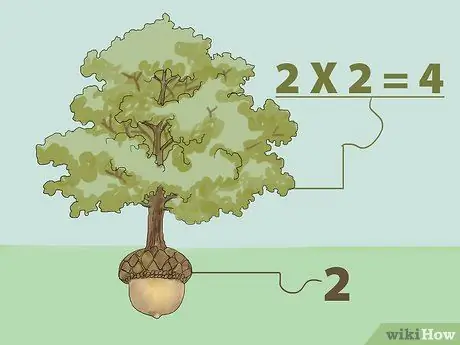
Steg 1. Hitta den perfekta kvadratroten genom att multiplicera
Kvadratroten i ett tal är ett tal som, när det multipliceras med sig själv, returnerar det ursprungliga talet. Med andra ord: "Vilket tal kan vi multiplicera med sig själva för att få det tal vi vill ha?"
- Till exempel är kvadratroten på 1 1 eftersom 1 multiplicerat med 1 är 1 (1X1 = 1). Således är kvadratroten på 4 2 eftersom 2 multiplicerat med 2 är 4 (2X2 = 4). Tänk på kvadratrotsbegreppet som ett träd. Ett träd växer från frö. Så, ett träd är större än ett frö, som växer från ett frö som är dess rot. Från exemplet ovan är 4 trädet och 2 är fröet.
- Så kvadratroten på 9 är 3 (3X3 = 9), av 16 är 4 (4X4 = 16), av 25 är 5 (5X5 = 25), av 36 är 6 (6X6 = 36), av 49 är 7 (7X7 = 49), från 64 är 8 (8X8 = 64), från 81 är 9 (9X9 = 81) och från 100 är 10 (10X10 = 100).
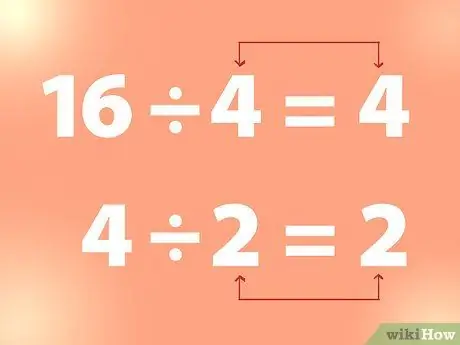
Steg 2. Använd kontinuerlig division för att hitta kvadratroten
För att hitta kvadratroten i ett heltal kan du dela heltalet med ett tal tills du får ett tal som är lika med divisorn.
- Exempel: 16 dividerat med 4 är 4. Och 4 dividerat med 2 är 2, och så vidare. Från exemplet ovan är 4 alltså kvadratroten på 16 och 2 är kvadratroten på 4.
- Perfekta kvadratrötter har inga bråk eller decimaler eftersom de är heltal.
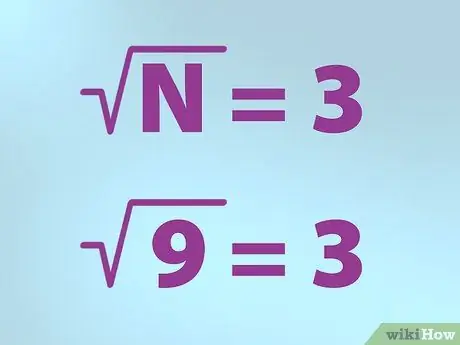
Steg 3. Använd rätt symbol för kvadratroten
Matematiker använder en särskild symbol för att representera kvadratroten. Formen är som en bock med plus en linje längst upp till höger.
- N är det tal som du vill hitta kvadratroten för. N är placerat under bockmarkeringen.
- Så, om du vill hitta kvadratroten på 9, skriv en formel genom att sätta "N" (9) inuti en bock (symbol "rot") skriv sedan ett likhetstecken och följt av 3. Det betyder "kvadratrot av 9 är lika med 3 ".
Metod 2 av 3: Hitta kvadratroten av ett annat nummer
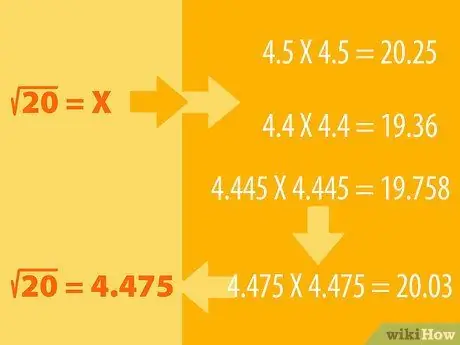
Steg 1. Gissa, och gör processen med eliminering
Det är svårt att hitta kvadratroten i ett icke-heltal. Det betyder dock inte att det är omöjligt.
- Säg till exempel att du vill hitta kvadratroten på 20. Vi vet att 16 är en perfekt kvadrat vars kvadratrot är 4 (4X4 = 16). Då är de 25 kvadratrötterna 5 (5X5 = 25), så kvadratroten på 20 måste ligga mellan de två.
- Du kan gissa att kvadratroten på 20 är 4,5. Nu kvadrat 4,5 för att se resultatet. Det vill säga att vi multiplicerar 4, 5 med sig själva: 4, 5X4, 5. Se om svaret är mer eller mindre än 20. Om din gissning är för långt, prova ett annat tal (t.ex. 4, 6 eller 4, 4) och justera gissa därefter tills du får nummer 20.
- Till exempel 4, 5X4, 5 = 20, 25, så logiskt måste vi hitta ett mindre tal, kanske 4, 4. 4, 4X4, 4 = 19, 36. Så kvadratroten på 20 måste ligga mellan 4, 5 och 4, 4. Försök med 4, 445X4, 445. Resultatet är 19, 758. Resultatet närmar sig. Fortsätt försöka med andra nummer tills du får 4, 475X4, 475 = 20, 03. Avrundat, det talet är 20.

Steg 2. Använd medelvärdesprocessen
Denna process börjar också med att hitta de två närmaste perfekta rutorna som flankeras av talet.
- Dela sedan det numret med en av de perfekta kvadratrötterna. Ta svaret, hitta sedan genomsnittet mellan det numret och det tal du vill hitta roten till (du kan hitta genomsnittet genom att lägga ihop de två och dela med två). Dela sedan det ursprungliga talet med det erhållna genomsnittet. Det sista steget, hitta genomsnittet av resultaten med genomsnittet beräknat första gången.
- Låter komplicerat? Det skulle vara lättare om det ges ett exempel. Till exempel ligger 10 mellan de två perfekta rutorna 9 (3X3 = 9) och 16 (4X4 = 16). Kvadratrötterna på båda siffrorna är 3 och 4. Så, dela 10 med det första talet, 3. Resultatet är 3, 33. Hitta nu genomsnittet på 3 och 3, 33 genom att lägga dem ihop och dela med 2. Resultatet är 3, 1667 Dela nu 10 med 3.1667. Resultatet är 3.1579. Hitta sedan genomsnittet på 3.1579 och 3.1667 genom att lägga ihop dem och dela med 2. Resultatet är 3.1623.
- Kontrollera ditt resultat genom att multiplicera svaret (i detta exempel 3, 1623) med sig själv. Resultatet av 3.1623 multiplicerat med 3.1623 visar sig vara 10.001.
Metod 3 av 3: Kvadrering av negativa tal
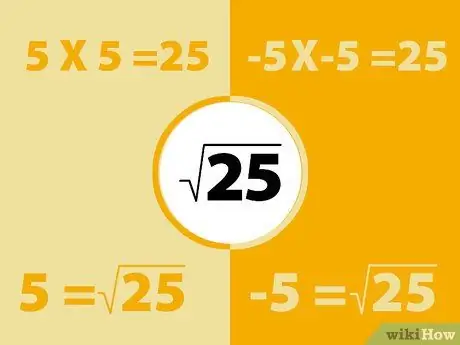
Steg 1. Fyrkantiga negativa tal med samma metod
Kom ihåg att negativa gånger negativa är positiva. Så kommer kvadraten med ett negativt tal att producera ett positivt tal.
- Till exempel -5X -5 = 25. Kom dock ihåg också att 5x5 = 25. Så kvadratroten på 25 kan vara -5 eller 5. I princip har varje tal två kvadratrötter.
- På samma sätt är 3X3 = 9 och -3X -3 = 9, så kvadratrötterna på 9 är 3 och -3. Den positiva kvadratroten kallas "huvudrot". Vid denna tidpunkt behöver vi bara uppmärksamma detta svar.
Steg 2. Använd en räknare
Även om det är bäst att kunna räkna för hand, finns det många onlinekalkylatorer tillgängliga för beräkning av kvadratrötter.
- Leta efter kvadratrotknappen på en vanlig miniräknare.
- I onlinekalkylatorn anger du direkt det nummer som du vill hitta kvadratrotsvärdet för och klickar på knappen. Datorn visar dig kvadratrotsvärdet.
Tips
-
Tänk alltid på några viktiga perfekta rutor:
- 02 = 0, 12 = 1, 32 = 9, 42 = 16, 52 = 25, 62 = 36, 72 = 49, 82 = 64, 92 = 81, 102 = 100,
- Kom också ihåg detta perfekta torg: 112 = 121, 122 = 144, 132 169, 142 = 196, 152 = 225, 162 = 256, 172 = 289…
- Observera också detta: 102 = 100, 202 = 400, 302 = 900, 402 = 1600, 502 = 2500, …






