- Författare Jason Gerald [email protected].
- Public 2024-02-01 14:15.
- Senast ändrad 2025-01-23 12:48.
Processen för att bestämma kvadratcentimeter (skriven som i2) på alla områden i tvådimensionella figurer är vanligtvis ganska enkla. För det enklaste fallet, när figuren är en kvadrat eller fyrkant, kan ytan i tum i kvadrat erhållas med formeln längd × bredd.
Ytorna i andra planformer (cirklar, trianglar etc.) kan beräknas med hjälp av olika matematiska formler. Du kan också göra en enkel omvandling av fötter i kvadrat eller centimeter i kvadrat från tum i kvadrat, om det behövs.
Steg
Metod 1 av 3: Bestämning av fyrkantiga tum på en kvadrat eller kvadrat
Steg 1. Bestäm längden på det område som ska mätas
Kvadrater och rektanglar har 4 raka sidor. En kvadrat har fyra sidor som är lika långa, medan i en rektangel är endast de motsatta sidorna lika långa. Mät ena sidan av rutan eller rektangeln för att ta reda på längdvärdet.
Steg 2. Bestäm bredden på det område som ska mätas
Mät sedan en av sidorna bredvid sidan som tidigare mätts. Denna sida ska möta den första sidan i en 90 graders vinkel. Detta är bredden på din kvadrat eller rektangel.
Eftersom alla fyra sidorna på rutan är lika långa kommer den resulterande "längden" att vara lika med "bredd" -måttet. Så, vanligtvis för en kvadrat behöver du bara mäta ena sidan
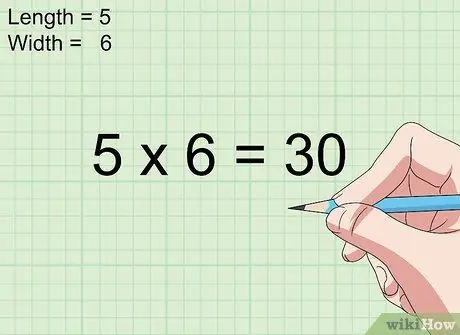
Steg 3. Multiplicera längden och bredden
Multiplicera helt enkelt längd- och breddmåtten för att bestämma ytan på en kvadrat eller rektangel i tum i kvadrat.
- Säg till exempel att problemet ber om arean av en rektangel som är 4 tum lång och 3 tum bred. I detta fall är rektangelns area 4 x 3 = 12 tum i kvadrat.
- Återigen har alla sidor på torget samma sidolängd. Så du behöver bara mäta ena sidan och multiplicera den med själva numret (även känt som "kvadrering" eller med två) för att få området i tum i kvadrat.
Metod 2 av 3: Bestämning av fyrkantiga tum på andra plana former
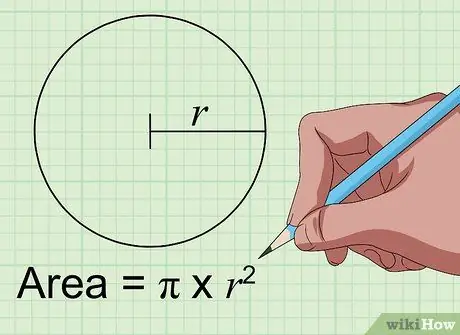
Steg 1. Hitta området för en cirkel med formeln Area = pi × r2.
För att hitta området för en cirkel i tum i kvadrat behöver du bara veta avståndet från cirkelns mitt till dess sidor i tum. Detta avstånd kallas cirkelns "radie". Om du har fått det anger du bara numret i variabeln "r" i ovanstående formel. Multiplicera med själva talet och multiplicera sedan med konstanten pi (3, 1415926 …) för att få cirkelns yta i tum i kvadrat.
Så en cirkel med en radie på 4 tum har en yta på 50,27 tum i kvadrat vilket är produkten av 3,14 x 16
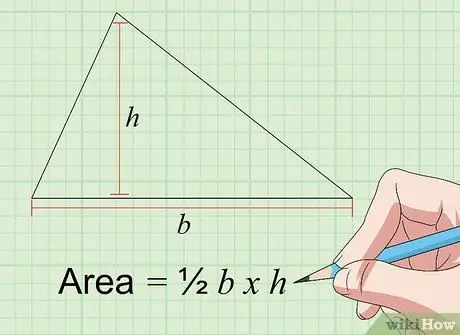
Steg 2. Hitta triangelns yta med formeln Area = 1/2 a × t
Arean av en triangel i tum i kvadrat kan hittas genom att multiplicera basen ("a") och höjden ("t"), som båda är i tum. Basen i en triangel är längden på en av dess sidor, medan "höjden" på en triangel är avståndet från sidan av "basen" till hörnet av triangeln motsatt den i 90 graders vinkel. Ytan på en triangel kan beräknas om du känner till längden på basens sidor och höjden på de tre sidorna och vinklarna mittemot dem.
Således, om du väljer en sida som är 4 tum lång som basen, och höjden på den sidan av basen är 3 tum, är triangelns yta 2 x 3 = 6 tum i kvadrat
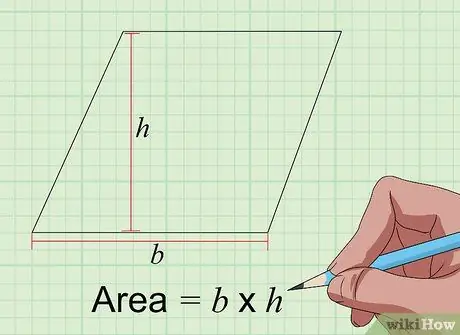
Steg 3. Hitta området för parallellogrammet med formeln Area = a × t
Ett parallellogram liknar en rektangel, men sidorna möts inte i 90 graders vinkel. Sättet att hitta området för ett parallellogram i tum i kvadrat är dock samma som för en rektangel, genom att multiplicera basen med höjden i tum. Basen är längden på en av dess sidor, medan höjden är avståndet från basens sida till den motsatta sidan i en vinkel på 90 grader.
Därför, om längden på den valda sidan är 5 tum, och efter att ha mätt höjden är den 4 tum lång, är området 5 x 4 = 20 tum i kvadrat
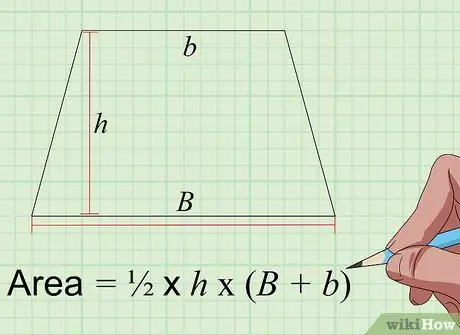
Steg 4. Hitta området för trapetsformen med formeln Area = 1/2 × t × (A+a)
En trapets är en fyrsidig platt form med ett par parallella sidor och de andra icke-parallella sidorna. För att beräkna arean på en trapets i tum i kvadrat måste du veta tre mått i tum, längden på den långa parallella sidan ("A"), den kortare parallella sidan ("a") och höjden av trapets ("t")., dvs avståndet mellan två parallella sidor mätt i 90 graders vinklar. Lägg till längden på de två parallella sidorna, multiplicera med höjden och dela sedan med två för att få trapezoidens yta i tum i kvadrat.
Till exempel, om de parallella sidorna av en trapets är 6 tum långa, de korta parallella sidorna är 4 tum och höjden är 5 tum, är ytan x 5 x (6+4) = 25 kvadratmeter
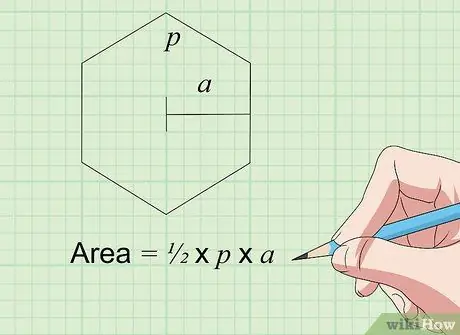
Steg 5. Hitta området för hexagon (hexagon) med formeln Area = × K × s
Denna formel fungerar för alla vanliga hexagoner, som är platta former som har 6 lika sidor och 6 lika vinklar. K är omkretsen, eller sidlängden gånger 6 (6 x s) för en vanlig sexkant. Variabeln a representerar apoten, som är längden från sexkantens mitt till en av dess sidor (mittpunkten för sidan mellan de två vinklarna). Multiplicera och dela resultatet för att hitta sexkantens yta.
Om en hexagon med alla sex sidor är 4 tum lång (vilket betyder K = 6 x 4 = 24) och apoten är 3,5 tum lång, är ytan x 24 x 3,5 = 42 kvadratmeter
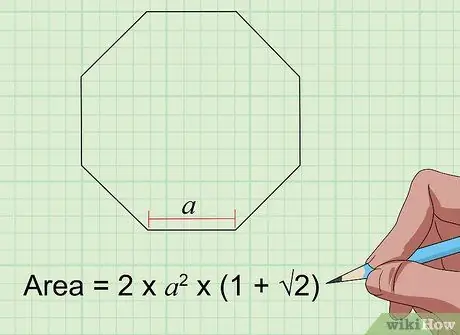
Steg 6. Hitta arean på oktagonen med formeln Area = 2s² × (1 + 2)
För en vanlig åttkant (som har 8 lika sidor och 8 vinklar) behöver du bara veta längden på ena sidan (“s” i formeln) för att hitta området. Anslut värdena till formeln och räkna ut dem för att få arean på oktagonen.
Om din vanliga åttkant har en sidolängd på 4 tum är dess yta 2 (16) x (1 + 1, 4) = 32 x 2,4 = 76,8 kvadratmeter
Metod 3 av 3: Konvertera andra enheter till kvadrattum

Steg 1. Ändra storleken till tum innan du beräknar
För att få ett slutligt svar i tum i kvadrat, rekommenderar vi att du konverterar alla värden som ska beräknas till tum (som längd, höjd eller apotem). Om kvadratets sidor är 1 fot vardera, konvertera dem till 12 tum innan du beräknar ytan. Följande konverteringsfaktorer används vanligtvis för att konvertera till tum:
- 1 fot = 12 tum
- 1 gård = 36 tum
- 1 centimeter = 0,3937 tum
- 1 meter = 39.3701 tum
- 1 millimeter = 0,0394 tum
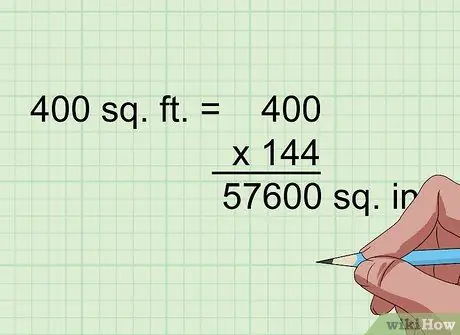
Steg 2. Multiplicera med 144 för att konvertera kvadratfot till kvadratmeter
1 fot i kvadrat är 1 fot i kvadrat (1 fot gånger 1 fot); vilket innebär att 12 tum i kvadrat också är 12 tum gånger 12 tum, vilket gör 144 tum i kvadrat. Så, om en platt form har en yta i fot i kvadrat, multiplicera den helt enkelt med 144 för att konvertera den till tum i kvadrat.
Till exempel 400 fot i kvadrat = 400 x 144 = 57 600 tum i kvadrat
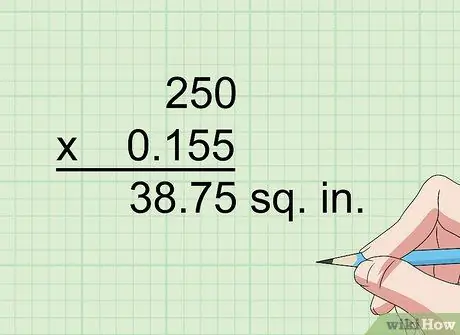
Steg 3. Multiplicera med 0,155 för att konvertera kvadratcentimeter till kvadratcentimeter
En centimeter är 0,394 tum och 0,394 kvadrat (0,394 x 0,394) lika med 0,155. Så, till exempel, om du behöver konvertera 250 centimeter i kvadrat till tum i kvadrat, multiplicera 250 med 0,155 för att få 38,75 tum i kvadrat.






