- Författare Jason Gerald [email protected].
- Public 2023-12-16 11:40.
- Senast ändrad 2025-01-23 12:47.
Det finns många olika former av platta former och det finns många anledningar till varför du kanske vill beräkna area: från att göra läxor till att uppskatta hur mycket färg som behövs för att måla om ett vardagsrum. Oroa dig inte, wikiHow har svaret! Börja från steg 1 nedan för att veta hur man beräknar arean på en planfigur.
Steg
Metod 1 av 7: Kvadrat, rektangel och parallellogram
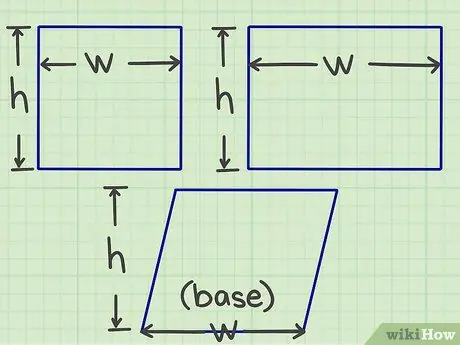
Steg 1. Mät längd och bredd
Börja mäta eller räkna ut längden och bredden på den platta formen (eller med andra ord storleken på var och en av de två sidorna som möts vid en punkt).
- För ett parallellogram måste du hitta basen och höjden, men i enkla termer är tanken densamma som längd och bredd.
- I den verkliga världen kan du behöva mäta det själv, men när det gäller att göra läxor har läraren vanligtvis redan skrivit ner siffrorna tillsammans med en bild av formen.
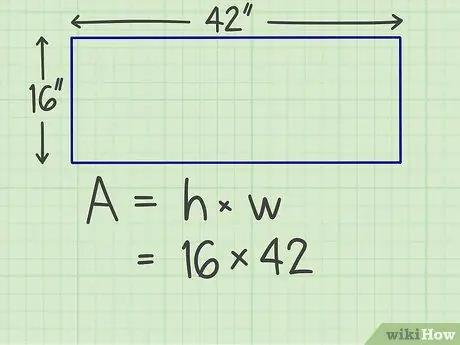
Steg 2. Multiplicera sidorna
Multiplicera den ena sidan med den andra. Anta till exempel att du har en rektangel med en bredd på 16 tum och en längd på 42 tum, så du måste beräkna 16 x 42.
Om du beräknar arean på en kvadrat (tidigare en kvadrat) kan du spara tid genom att kvadrera en av sidorna med en miniräknare. Om sidan mäter 4 m, tryck på 4 -knappen och tryck sedan på fyrkantstangenten på miniräknaren för att visa resultatet. Kvadrat betyder att man multiplicerar ett tal med sig själv
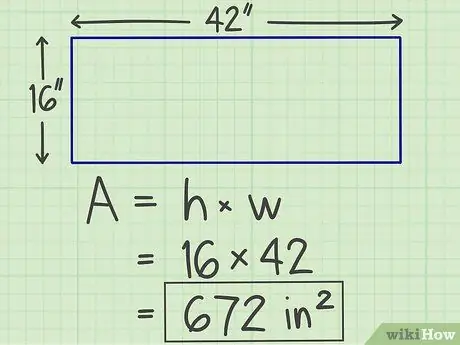
Steg 3. Skriv ner resultaten
Multiplikationen du gjorde tidigare kommer att producera ett tal, vilket är arean på planet du beräknar, med enheten "kvadrat". Således har rektangeln som vi beräknade tidigare en yta på 672 kvadratmeter.
Ibland skrivs denna kvadratiska enhet också som en liten 2 som stiger något efter enhetsnamnet (som skrivkrafter)
Metod 2 av 7: Trapezoid
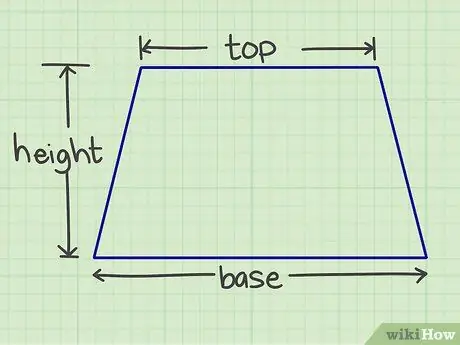
Steg 1. Mät önskat antal
Du måste mäta basen, taket och höjden. Basen och taket är parallella sidor, medan höjden är en vinkelrät linje som förbinder de två parallella sidorna.
I den verkliga världen kan du behöva mäta det själv, men när det gäller att göra läxor har läraren vanligtvis redan skrivit ner siffrorna tillsammans med en bild av formen
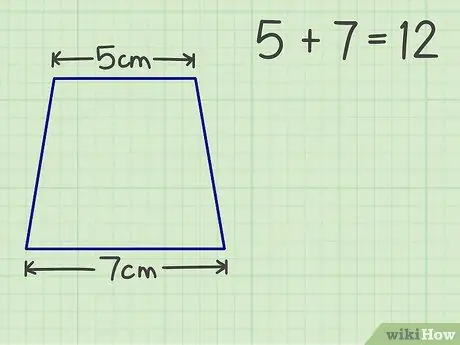
Steg 2. Lägg ihop de två parallella sidorna
Till exempel har vår trapets ett tak på 5 cm och en bas på 7 cm. Summan av de två parallella sidorna är 12.
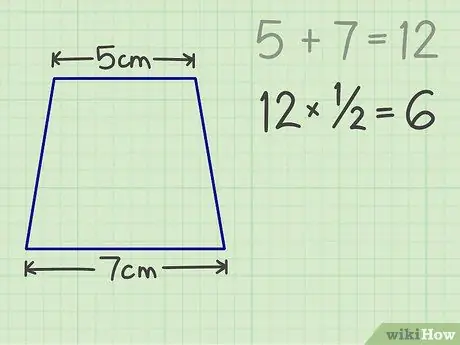
Steg 3. Multiplicera talet med 1/2, resultatet är 6
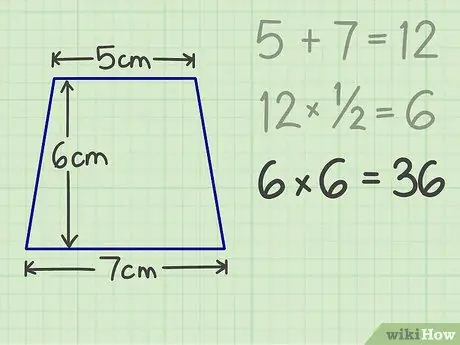
Steg 4. Därefter multiplicerar du resultatet med höjden
Till exempel, om en trapets har en höjd av 6 cm är slutresultatet 36.
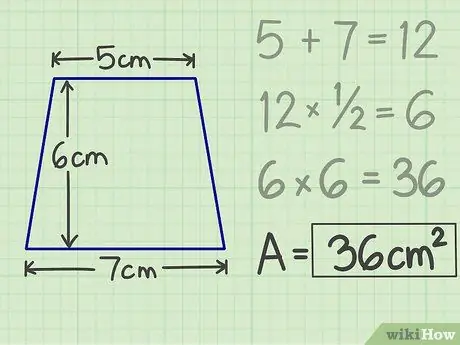
Steg 5. Skriv ner resultaten
Multiplikationen du gjorde tidigare kommer att producera ett tal, nämligen trapezoidens yta. Så för en trapets med ett tak på 5 cm, en bas på 7 cm och en höjd på 6 cm är området 36 cm kvadrat.
Metod 3 av 7: Cirkel
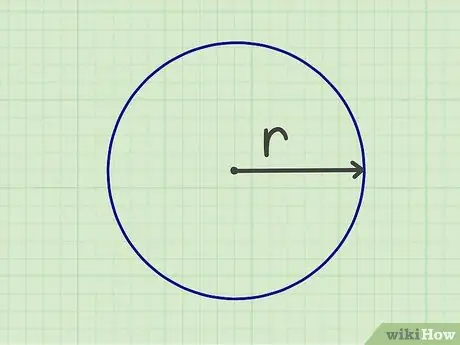
Steg 1. Mät radien
För att kunna beräkna arean på en cirkel måste du mäta radien. radien är avståndet från cirkelns mitt till dess kant. Du kan också mäta radien genom att mäta diametern (cirkelns bredd från kant till kant) och sedan dela antalet med två.
I den verkliga världen kan du behöva mäta det själv, men när det gäller att göra läxor har läraren vanligtvis redan skrivit ner siffrorna tillsammans med en bild av formen
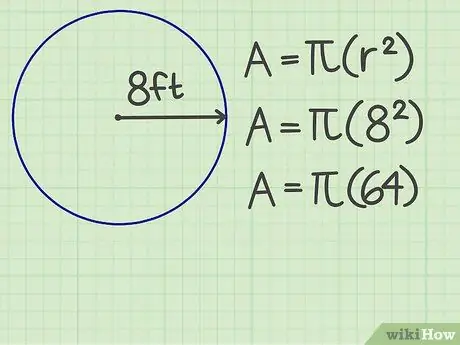
Steg 2. Fyrkantiga fingrarna
Multiplicera antalet radier med sig själv. Till exempel är radiens radie 8 fot, så resultatet är 64.
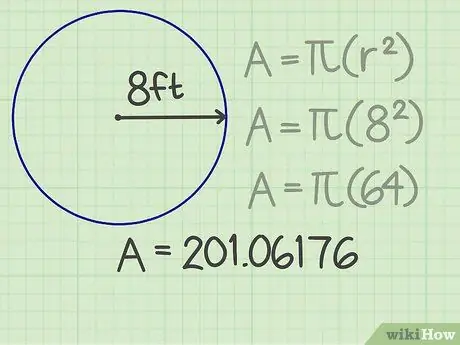
Steg 3. Multiplicera resultatet med pi
Pi (π) är ett viktigt tal som används i olika formler. Om du använder en miniräknare, tryck på pi -tangenten för att få riktigt exakta resultat. Annars, för att göra dina beräkningar enklare, kan du avrunda pi till några siffror efter komma, till exempel 3, 14159. När du multiplicerar detta tal med kvadraten i radien blir resultatet 201, 06176.
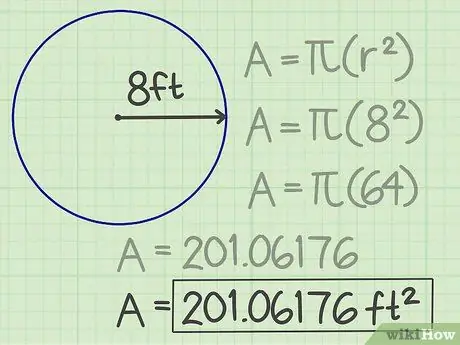
Steg 4. Skriv ner resultaten
Antalet erhållna, 201, 06176 är cirkelns yta. Således är dess yta 201 06176 kvadratfot.
Metod 4 av 7: Sektor (Juring)
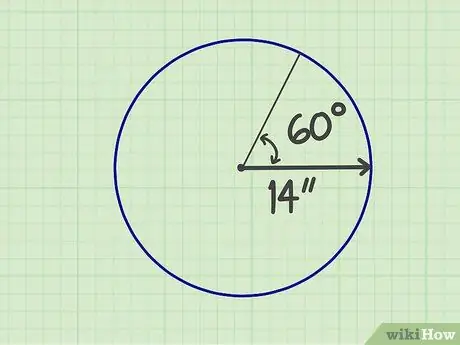
Steg 1. Mät de önskade siffrorna
En sektor är en sektion av en cirkel som bildas av två radier och en kant, så att formen är som en fläkt. Du måste veta storleken på radien och vinkeln som utgör "fläkten". Anta till exempel att en sektor har en radie på 14 tum och en vinkel på 60 grader.
I den verkliga världen kan du behöva mäta det själv, men när det gäller att göra läxor har läraren vanligtvis redan skrivit ner siffrorna tillsammans med en bild av formen
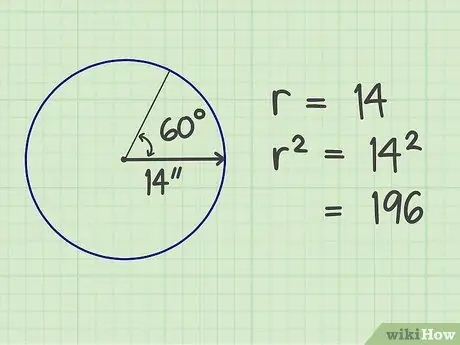
Steg 2. Fyrkantiga fingrarna
Multiplicera antalet radier med sig själv. Resultatet är 196 (14x14).

Steg 3. Multiplicera resultatet med pi
Pi (π) är ett viktigt tal som används i olika formler. Om du använder en miniräknare, tryck på pi -tangenten för att få riktigt exakta resultat. Annars, för att göra dina beräkningar enklare, kan du avrunda pi till några siffror efter kommatecken, till exempel 3, 14159. Om du multiplicerar detta tal med kvadraten i radien blir resultatet 615, 75164.

Steg 4. Dela vinkelns mått med 360
Dela sektorfläktvinkeln med 360 (måttet på en helcirkelvinkel). För exemplet ovan är resultatet cirka 0,166. Om du beräknar det med en miniräknare är resultatet faktiskt längre och iterativt, men här avrundas det för att göra beräkningen enklare.

Steg 5. Multiplicera detta nummer med föregående nummer
Multiplicera det tal du får när du dividerar vinkeln med 360, med det tal du fick tidigare efter att ha multiplicerat pi med kvadraten i radien. för exemplet ovan är resultatet 102, 214 (efter avrundning).
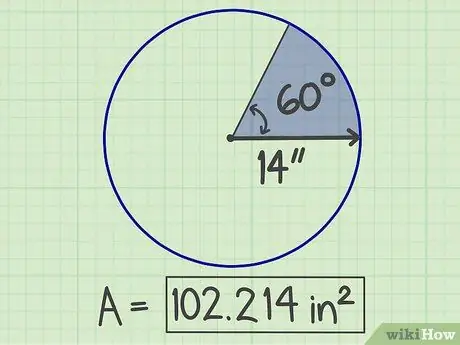
Steg 6. Skriv ner resultaten
Det erhållna antalet är sektorns yta, som är 102, 214 kvadratmeter.
Metod 5 av 7: Ellips
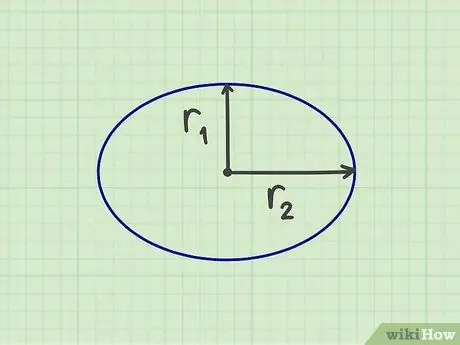
Steg 1. Mät önskat antal
För att beräkna ytan på en ellips måste du mäta två "radier", nämligen den korta radien och den långa radien, som är halva bredden och hälften av ellipsens höjd. Du kan också mäta den korta radien från ellipsens mitt till den kortaste sidan och den långa radien från ellipsens mitt till den längsta sidan. Den korta radien ska bilda en rät vinkel mot den långa radien.
I den verkliga världen kan du behöva mäta det själv, men när det gäller att göra läxor har läraren vanligtvis redan skrivit ner siffrorna tillsammans med en bild av formen
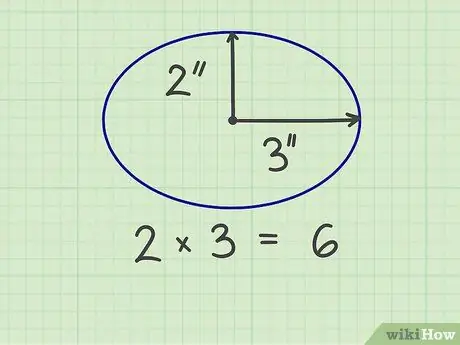
Steg 2. Multiplicera de två fingrarna
Till exempel är en ellips 6 tum bred och 4 tum hög, så radierna är 3 tum och 2 tum. När de två talen multipliceras blir resultatet 6 (3 x 2).

Steg 3. Multiplicera resultatet med pi
Pi (π) är ett viktigt tal som används i olika formler. Om du använder en miniräknare, tryck på pi -tangenten för att få riktigt exakta resultat. Annars, för att göra dina beräkningar enklare, kan du avrunda pi till några siffror efter komma, till exempel 3, 14159. När du multiplicerar detta tal med kvadraten i radien blir resultatet 18, 84954.
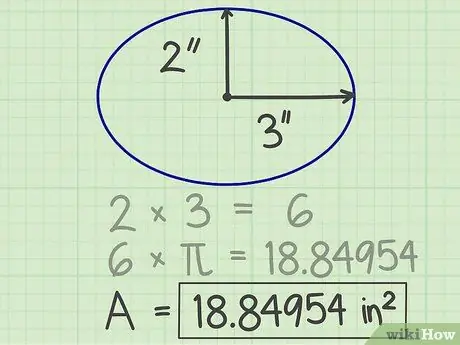
Steg 4. Skriv ner resultaten
Antalet som erhålls från beräkningen ovan är ellipsens yta. I exemplet ovan är ellipsens yta 18,84954 kvadratmeter.
Metod 6 av 7: Triangel
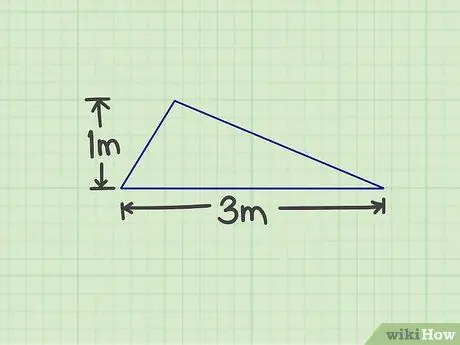
Steg 1. Mät önskat antal
Du måste mäta basen och höjden på triangeln. Vilken sida av triangeln som helst kan vara basen, så länge du kan mäta höjden. Till exempel finns det en triangel med en bas på 3 m och en höjd av 1 m.
I den verkliga världen kan du behöva mäta det själv, men när det gäller att göra läxor har läraren vanligtvis redan skrivit ner siffrorna tillsammans med en bild av formen
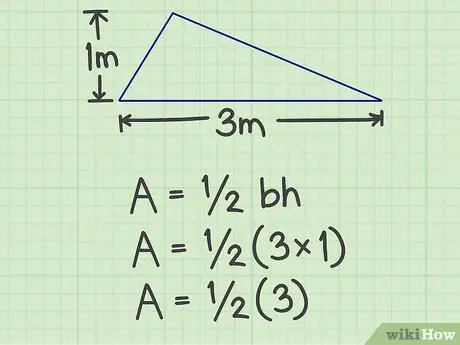
Steg 2. Multiplicera basen med höjden
För exemplet ovan är resultatet 3 (3x1).
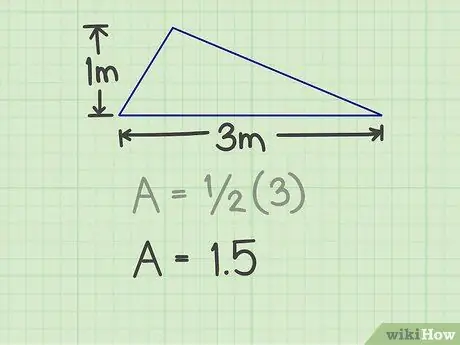
Steg 3. Multiplicera resultatet med 1/2
Denna multiplikation ger siffrorna 1, 5.
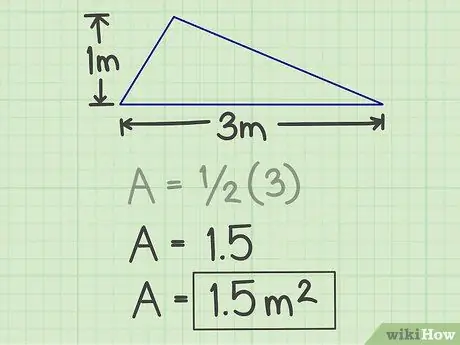
Steg 4. Skriv ner resultaten
Antalet som genereras av beräkningen ovan är triangelns yta, och med exemplet ovan är dess yta 1,5 kvadratmeter.
Metod 7 av 7: Komplex platt byggnad
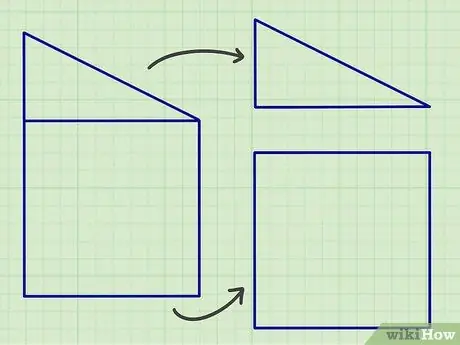
Steg 1. Separera komplexa planformer i delar som består av de geometriska standardformerna ovan
Om det du gör är läxor, kan det vara lätt att dela den komplexa formen i de platta former som diskuterats tidigare, men i verkligheten kan du behöva dela den platta formen i massor av platta former för att få ett korrekt beräkningsresultat.
Ett bra sätt att börja är att leta efter linjer som är parallella eller som bildar en viss vinkel, eftersom de flesta plana former består av dessa former
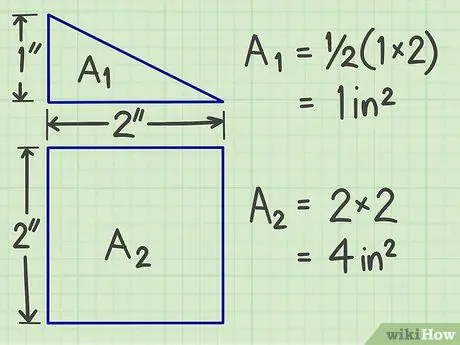
Steg 2. Beräkna ytan för var och en av de planfigurer som härrör från separationen
Använd metoderna ovan för att få området för varje platt form.
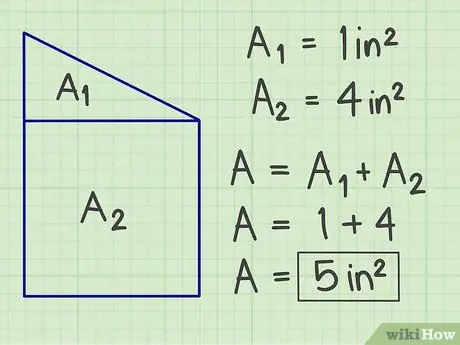
Steg 3. Lägg till resultaten
Lägg ihop alla beräknade områden för att få den totala ytan av din komplexa planfigur.
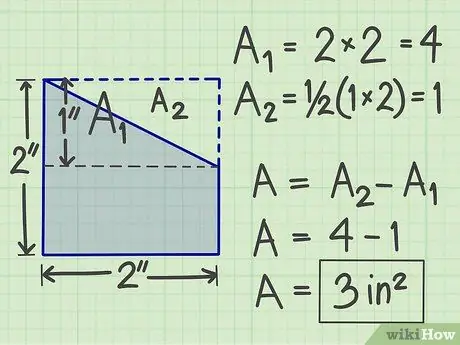
Steg 4. Använd en annan metod
Det finns många andra sätt du kan prova, beroende på formen på den komplexa plattformen. Till exempel kan du också lägga till en tänkt plan form till den så att den blir en standard geometrisk plan form. Beräkna sedan ytan, subtrahera sedan ytan på den imaginära plattform som du brukade lägga till.
Tips
- Använd den här miniräknaren om du behöver hjälp med att lösa matematiska beräkningar.
- Be en vän om hjälp om du fortfarande har problem!
Varning
- Det är alltid bättre att dubbelkolla beräkningsresultaten för att se till att de är korrekta!
- Se till att enheterna du använder är desamma (cm, m, tum, etc.) vid beräkning, så att du inte blir felberäknad på grund av blandade enheter!






