- Författare Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:24.
- Senast ändrad 2025-01-23 12:47.
Tyngdkraften är en av de grundläggande krafterna i fysiken. Den viktigaste aspekten av gravitationen är att den är universell: alla objekt har en gravitationskraft som lockar andra objekt. Gravitationskraftens storlek beror på massan och avståndet mellan de två föremålen.
Steg
Del 1 av 2: Beräkning av tyngdkraften mellan två objekt

Steg 1. Definiera ekvationen för gravitationskraften som drar på ett objekt, Fgrav = (Gm1m2)/d2.
För att kunna beräkna ett objekts gravitationskraft tar denna ekvation också hänsyn till massorna av de två föremålen och deras avstånd från varandra. Ekvationsvariablerna beskrivs nedan.
- Fgrav är gravitationskraften
- G är den universella gravitationskonstanten 6.673 x 10-11 Nm2/kg2
- m1 är massan av det första objektet
- m2 är massan av det andra objektet
- d är avståndet mellan de två föremålens centrum
- Ibland hittar du bokstaven r istället för d. Dessa två symboler representerar avståndet mellan de två föremålen.

Steg 2. Använd lämpliga metriska enheter
För denna ekvation måste du använda metriska enheter. Objektets massa måste vara i kilogram (kg) och avståndet mellan föremålen måste vara i meter (m). Du måste konvertera dessa enheter till metriska enheter innan du fortsätter

Steg 3. Bestäm massan av objektet i fråga
För små föremål kan du väga dem för att bestämma deras vikt i kilogram. För stora föremål kan du slå upp den ungefärliga massan på ett bord eller på internet. I fysikproblem kommer vanligtvis massan av objektet att berättas.

Steg 4. Mät avståndet mellan de två föremålen
Om du försöker beräkna gravitationskraften mellan ett objekt och jorden måste du veta hur långt detta objekt är från jordens centrum.
- Avståndet från jordens yta till jordens centrum är cirka 6,38 x 106 m.
- Du kan leta upp tabeller eller andra källor på internet som berättar det ungefärliga avståndet från jordens mitt till objekt på olika höjder på jordytan.

Steg 5. Slutför beräkningen
Om du har definierat variablerna i ekvationen, ange dem gärna för att lösa. Se till att alla variabler finns i metriska enheter och är korrekt skalade. Massan måste vara i kilogram och avståndet måste vara i meter. Lös ekvationer i rätt beräkningsordning.
- Till exempel bestämma gravitationskraften hos en person vars massa är 68 kg över jordens yta. Jordens massa är 5,98 x 1024 kg.
- Se till att alla variabler är i rätt enheter. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6,673 x 10-11 Nm2/kg2och d = 6, 38 x 106 m
- Skriv din ekvation: Fgrav = (Gm1m2)/d2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)]/(6, 38 x 106)2
- Multiplicera massorna av de två objekten som beaktas. 68 x (5, 98 x 1024) = 4,06 x 1026
- Multiplicera resultatet m1 och M2 med gravitationskonstanten G. (4,06 x 1026) x (6,67 x 10-11) = 2 708 x 1016
- Kvadrera avståndet mellan de två föremålen. (6, 38 x 106)2 = 4,07 x 1013
- Aktieresultat G x m1 x m2 med avståndet i kvadrat för att erhålla gravitationskraften i Newton (N). 2, 708 x 1016/4, 07 x 1013 = 665 N
- Dess gravitationskraft är 665 N.
Del 2 av 2: Beräkning av tyngdkraften på jorden

Steg 1. Förstå Newtons andra lag, F = ma
Newtons andra lag säger att accelerationen av ett objekt är direkt proportionell mot nettokraften som verkar på det och omvänt proportionell mot dess massa. Med andra ord, om en kraft som verkar på ett objekt är större än kraften som verkar i motsatt riktning, kommer objektet att röra sig med den starkare kraften.
- Denna lag kan summeras med ekvationen F = ma, där F är kraften, m är objektets massa och a är accelerationen.
- Tack vare denna lag kan vi beräkna gravitationskraften för alla objekt på jordens yta, med hjälp av den kända accelerationen på grund av gravitationen.
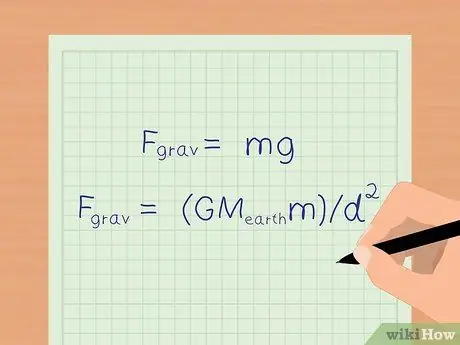
Steg 2. Hitta accelerationen på grund av jordens gravitation
På jorden gör tyngdkraften att alla föremål accelererar med 9,8 m/s2. På jordytan kan vi använda en förenklad ekvation: Fgrav = mg för att beräkna gravitationskraften.
Om du vill veta ett mer exakt antal gravitationskrafter kan du fortfarande använda formeln i föregående steg, Fgrav = (GMJordenm)/d2 för att bestämma gravitationskraften.

Steg 3. Använd lämpliga metriska enheter
För denna ekvation måste du använda metriska enheter. Objektets massa måste vara i kilogram (kg) och avståndet mellan föremålen måste vara i meter (m). Du måste konvertera dessa enheter till metriska enheter innan du fortsätter.

Steg 4. Bestäm massan av objektet i fråga
För små föremål kan du väga dem för att bestämma deras vikt i kilogram. För stora föremål kan du slå upp den ungefärliga massan på ett bord eller på internet. I fysikproblem kommer vanligtvis massan av objektet att berättas.

Steg 5. Slutför beräkningen
Om du har definierat variablerna i ekvationen, ange dem gärna för att lösa. Se till att alla variabler finns i metriska enheter och är korrekt skalade. Massan måste vara i kilogram och avståndet måste vara i meter. Lös ekvationer i rätt beräkningsordning.
- Låt oss försöka använda ekvationen i föregående steg och se hur nära resultaten är. Bestäm gravitationskraften hos en person med en massa på 68 kg på jordens yta.
- Se till att alla variabler har rätt enheter: m = 68 kg, g = 9,8 m/s2.
- Skriv ner formeln. Fgrav = mg = 68*9, 8 = 666 N.
- Med hjälp av formeln F = mg är gravitationskraften 666 N, medan resultatet från formeln i föregående steg är 665 N. Som du kan se är de två resultaten nästan desamma.
Tips
- Dessa två formler bör ge samma svar, men den kortare och enklare formeln är lättare att använda när man diskuterar objekt på en planets yta.
- Använd den första formeln om du inte känner till accelerationen på grund av gravitationen på en planet, eller om du beräknar gravitationskraften mellan två mycket stora objekt, till exempel månen eller planeter.






