Med Spearmans rangkorrelationskoefficient kan vi identifiera om två variabler har en monoton funktionsrelation (det vill säga när ett tal ökar kommer det andra talet också att öka, eller vice versa). För att beräkna Spearmans rangkorrelationskoefficient måste du rangordna och jämföra datamängder för att hitta d2och mata sedan in data i den standardiserade eller förenklade formeln för korreleringskoefficient för Spearman -rang. Du kan också beräkna dessa koefficienter med hjälp av Excel -formler eller kommandot R.
Steg
Metod 1 av 3: Manuellt sätt
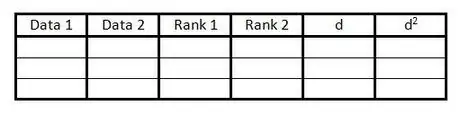
Steg 1. Skapa en tabell
Tabellen används för att inkludera all information som behövs för att beräkna Spearman Rank -korrelationskoefficienten. Du behöver ett bord så här:
- Skapa 6 kolumner med rubriker, som i exemplet.
- Förbered lika många tomma rader som antalet datapar.
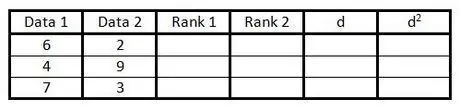
Steg 2. Fyll i de två första kolumnerna med datapar
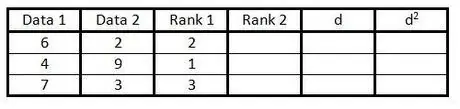
Steg 3. Ange rankningen av den första kolumnen med datagrupper i den tredje kolumnen från 1 till n (antal data)
Ge betyg 1 för det lägsta värdet, betyg 2 för nästa lägsta värde, och så vidare.
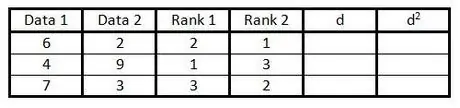
Steg 4. Gör detsamma som i steg 3 i den fjärde kolumnen, men för att ranka data i den andra kolumnen
-
Medel_742 Om det finns två (eller fler) data som har samma värde beräknar du det genomsnittliga betyget för datan och anger det sedan i en tabell baserat på detta medelvärde.
I exemplet till höger finns det två värden på 5 på betyg 2 och 3. Eftersom det finns två 5: or, hitta genomsnittet av betyg. Genomsnittet på 2 och 3 är 2,5, så ange ett värderingsvärde på 2,5 för båda värdena 5.
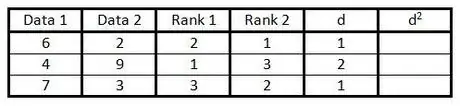
Steg 5. Beräkna skillnaden mellan de två siffrorna i rangkolumnen i kolumn "d"
Det vill säga, om en kolumn är rankad 1 och den andra kolumnen är rankad 3, är skillnaden 2. (Tecknet spelar ingen roll, eftersom nästa steg är att kvadrera värdet.)
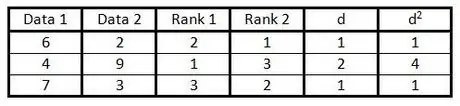
Steg 6. Kvadrera varje tal i kolumn "d" och skriv resultatet i kolumn "d2".
Steg 7. Lägg till all data i kolumn d2".
Resultatet är d2.
Steg 8. Välj en av följande formler:
-
Om ingen av värderingarna är desamma som i föregående steg anger du detta värde i den förenklade formeln för korreleringskoefficient för Spearman Rank
Steg 8_271 och ersätt "n" med antalet datapar för att få resultatet.
Steg9_402 -
Om det finns en liknande rang i föregående steg, använd standardformeln Spearman Rank Correlation Coefficient:
Spearman
Steg 9. Tolka resultaten
Värdet kan variera mellan -1 och 1.
- Om värdet är nära -1 är korrelationen negativ.
- Om värdet är nära 0 finns det ingen linjär korrelation.
- Om värdet är nära 1 är korrelationen positiv.
Metod 2 av 3: Använda Excel
Steg 1. Skapa en ny kolumn för data tillsammans med dess ranking
Till exempel, om din data finns i kolumn A2: A11, använd formeln "= RANK (A2, A $ 2: A $ 11)" och kopiera den tills den täcker alla kolumner och rader.
Steg 2. Ändra samma betyg som beskrivs i steg 3 och 4 i metod 1
Steg 3. I den nya cellen beräknar du korrelationen mellan de två rangkolumnerna med formeln "= CORREL (C2: C11, D2: D11)"
I detta exempel hänvisar C och D till kolumnen där rankningen finns. Den nya cellen kommer att fyllas med Spearman Rank Correlation.
Metod 3 av 3: Använda R
Steg 1. Installera R -programmet först om du inte redan har det
(Se
Steg 2. Spara dina data i CSV -formulär, lägg de data du vill hitta korrelationen i de två första kolumnerna
Vi kan göra detta genom att använda menyn "Spara som".
Steg 3. Öppna R Editor
Om du arbetar från terminalen, kör bara R. Om du arbetar från skrivbordet klickar du på ikonen R.
Steg 4. Skriv följande kommando:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv") och tryck på Enter.
- cast (rang (d [, 1]), rank (d [, 2]))
Tips
Data måste bestå av minst 5 par så att trenden kan ses (antalet data är 3 par i exemplet bara för att förenkla beräkningar.)
Varning
- Spearman rank -korrelationskoefficienten identifierar endast styrkan i korrelationen där data stiger eller faller konsekvent. Om det finns en annan trend i data, Spearmans rangkorrelation Nej kommer att ge en korrekt representation.
- Denna formel är baserad på antagandet att det inte finns några lika betyg. När det finns samma rang som i exemplet, bör vi använda den här definitionen: korrelationskoefficienten för multiplikationsmomentet efter rang.
