- Författare Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:24.
- Senast ändrad 2025-01-23 12:47.
Innan du beräknar spänningen över ett motstånd måste du först bestämma vilken typ av krets (sträng) som används. Om du behöver återgå till grundläggande termer eller behöver hjälp med att förstå elektriska kretsar, börja med det första avsnittet. Annars går du direkt till den typ av krets du vill arbeta med
Steg
Del 1 av 3: Förstå elektriska kretsar
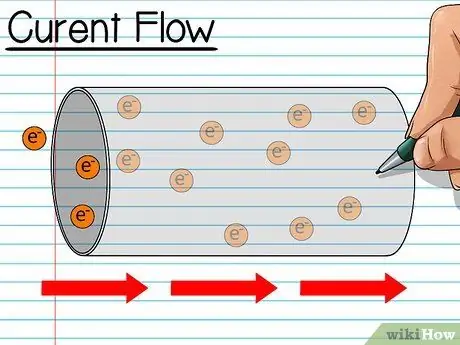
Steg 1. Lär dig om elektrisk ström
Du kan använda följande analogi: tänk dig att du häller spannmål i en skål. Varje spannmål är en elektron, och flödet av spannmål in i skålen är en elektrisk ström. När du pratar om elektricitet förklarar du det genom att säga hur många spannmålskorn som flödar varje sekund. När du talar om elektrisk ström mäter du den i enheter av ampere (ampere), vilket är ett visst antal elektroner (som är mycket stora värden) som flödar varje sekund.
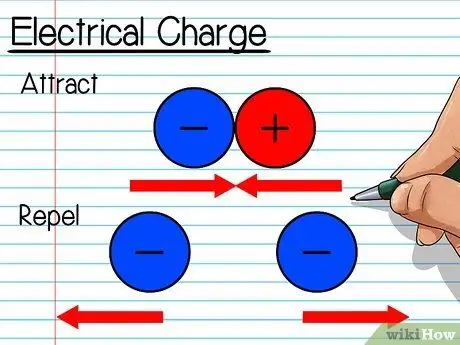
Steg 2. Vet om elektrisk laddning
Elektroner har en "negativ" elektrisk laddning. Det vill säga elektroner attraherar (eller flödar mot) positivt laddade objekt och stöter bort (eller flyter ifrån) negativt laddade objekt. Alla elektroner har en negativ laddning så att de alltid trycker på andra elektroner och sprider sig.
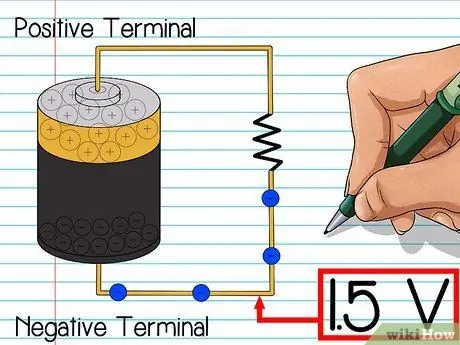
Steg 3. Förstå spänning
Spänning mäter skillnaden i elektrisk laddning mellan två punkter. Ju större skillnad, desto starkare lockar de två punkterna varandra. Här är ett exempel på hur du använder ett vanligt batteri:
- Inuti batteriet producerar de kemiska reaktionerna som uppstår en pool av elektroner. Dessa elektroner går till den negativa polen i batteriet, medan den positiva polen förblir nästan tom. Dessa kallas positiva och negativa terminaler. Ju längre denna process varar, desto större är spänningen mellan de två polerna.
- När du ansluter trådarna mellan de positiva och negativa polerna har elektronerna på den negativa polen nu någonstans att gå. Elektronerna vid den negativa polen flödar mot den positiva polen och producerar en elektrisk ström. Ju större spänning, desto fler elektroner rör sig till den positiva polen varje sekund.
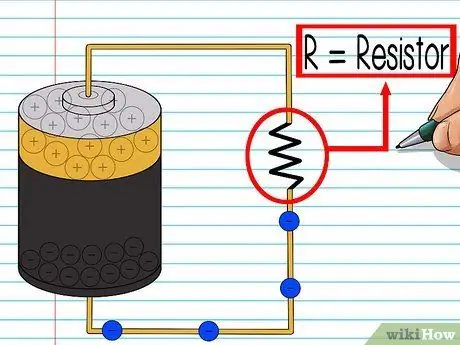
Steg 4. Lär dig mer om motstånd
Ett hinder är något som blockerar elektroner. Ju större motstånd, desto svårare är det för elektroner att passera. Motståndet saktar ner den elektriska strömmen eftersom antalet elektroner som passerar varje sekund minskar.
Motstånd kan vara vad som helst i en elektrisk krets som tillför motstånd. Du kan köpa riktiga "motstånd", men i problem representeras motstånd vanligtvis av glödlampor eller något som har motstånd

Steg 5. Memorera Ohms lag
Det finns ett enkelt samband mellan ström, spänning och elektrisk resistans. Skriv eller memorera följande formel eftersom du kommer att behöva den för att lösa problem relaterade till elektriska kretsar:
- Ström = spänning dividerat med motstånd
- Formeln kan skrivas enligt följande: I = V / R
- Tänk vad som händer om V (spänning) eller R (motstånd) i kretsen ökar. Är det i överensstämmelse med diskussionen ovan?
Del 2 av 3: Beräkning av spänningen genom ett motstånd (seriekrets)
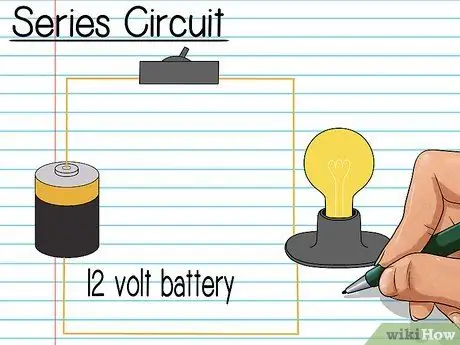
Steg 1. Förstå seriekretsar
Seriens elektriska kretsar är mycket lätta att upptäcka. Formen är i form av en kabelslinga med alla komponenter ordnade i rad längs kabeln. En elektrisk ström strömmar genom hela tråden och genom varje motstånd eller element som den möter.
- Elektrisk ström alltid densamma vid varje punkt i kretsen.
- Vid beräkning av spänning är motståndets placering i kretsen irrelevant. Du kan ta ett motstånd och flytta det över kretsen, och spänningen över varje motstånd förblir densamma.
- Vi kommer att använda ett exempel på en elektrisk krets med 3 motstånd i serie: R1, R2och R.3. Kretsen får ström från ett 12 volts batteri. Vi hittar spänningen över varje motstånd.
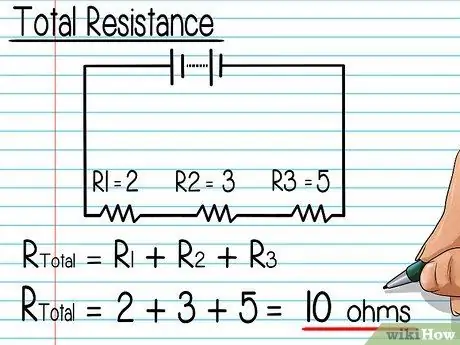
Steg 2. Beräkna det totala motståndet
Lägg ihop alla motståndsvärden i kretsen. Resultatet är seriekretsens totala motstånd.
Till exempel de tre motstånden R1, R2och R.3 har motstånd på 2 (ohm), 3 respektive 5. Således är det totala motståndet 2 + 3 + 5 = 10 ohm.

Steg 3. Hitta strömmen i kretsen
Använd Ohms lag för att hitta värdet av strömmen i en hel elektrisk krets. Kom ihåg att i en seriekrets är strömmen alltid densamma vid varje punkt i kretsen. Efter att ha fått det aktuella värdet kan vi utföra alla återstående beräkningar.
Ohms lag säger att nuvarande I = V / R. Spänningen över kretsen är 12 volt och kretsens totala motstånd är 10 ohm. Anslut dessa nummer till formeln för att få I = 12 / 10 = 1,2 ampere.
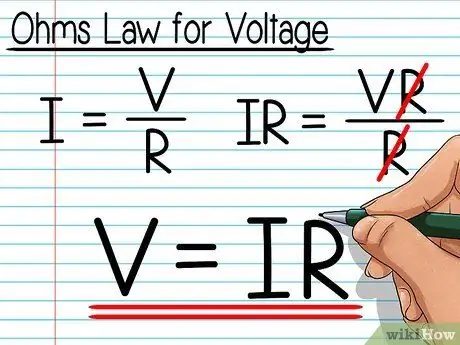
Steg 4. Justera Ohms lag för att hitta spänningsvärdet
Använd grundläggande algebra för att hitta värdet på spänning istället för ström:
- Jag = V / R
- IR = VR / R
- IR = V
- V = IR
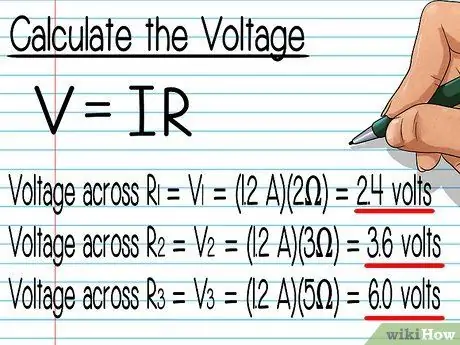
Steg 5. Beräkna spänningen över varje motstånd
Vi vet redan värdet av motstånd och ström. Nu kan vi göra alla beräkningar. Anslut siffrorna till formeln och slutför beräkningen. Här är beräkningarna för de tre motstånden från exemplet ovan:
- Spänning vid R1 = V1 = (1, 2A) (2Ω) = 2, 4 volt.
- Spänning vid R2 = V2 = (1, 2A) (3Ω) = 3,6 volt.
- Spänning vid R3 = V3 = (1, 2A) (5Ω) = 6 volt.
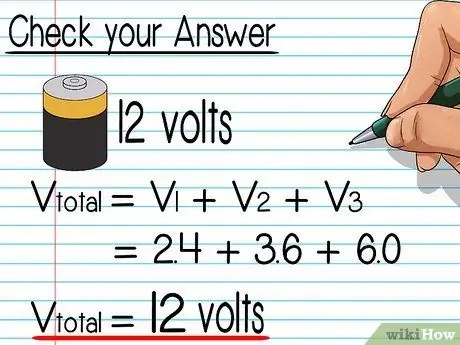
Steg 6. Kontrollera dina svar
I en seriekrets måste summan av alla svaren vara lika med den totala spänningen. Lägg till varje spänning du beräknade och kontrollera att den matchar kretsens totala spänning. Om inte, försök hitta felet i dina beräkningar.
- Enligt exemplet ovan är 2, 4 + 3, 6 + 6 = 12 volt, lika med den totala spänningen genom den elektriska kretsen.
- Om ditt svar är lite dåligt (säg 11, 97 istället för 12), är chansen stor att du har rundat siffror medan du arbetar med formler. Oroa dig inte, ditt svar är inte fel.
- Kom ihåg att spänning mäter skillnaden i laddning eller antalet elektroner. Tänk dig att du räknar de nya elektronerna som ses när de färdas längs en elektrisk krets. Om du räknar rätt vet du den totala förändringen i elektroner från början till slut.
Del 3 av 3: Beräkning av spänningen genom ett motstånd (parallell krets)
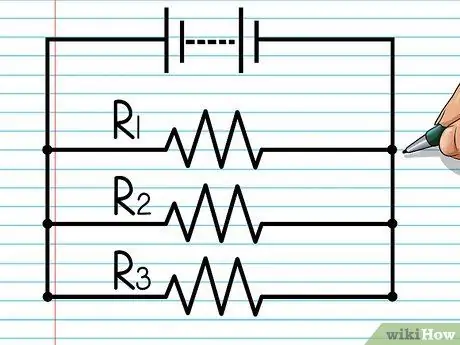
Steg 1. Lär dig om parallella kretsar
Föreställ dig en kabel som ansluts till en pol på batteriet och sedan förgrenas till två separata ledningar. Dessa två ledningar är parallella med varandra och ansluts sedan igen innan de ansluts till batteriets andra pol. Om ledningen till vänster är ansluten till ett motstånd, och ledningen till höger också är ansluten till ett annat motstånd, är de två motstånden anslutna "parallellt".
Du kan lägga till så många parallella kablar som du vill. Den här guiden kan användas för elektriska kretsar som förgrenar sig till 100 ledningar som sedan återansluts
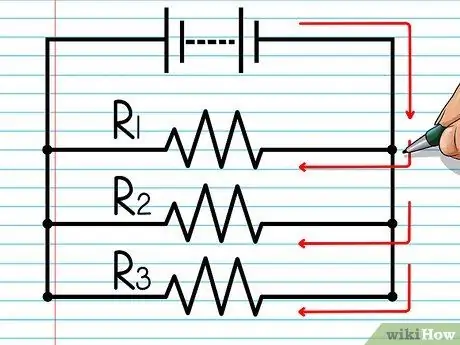
Steg 2. Vet hur elektrisk ström flödar i parallella kretsar
Elektrisk ström flödar genom alla tillgängliga banor. Elektrisk ström kommer att flöda genom tråden till vänster, genom motståndet till vänster och ända till andra änden. Samtidigt strömmar också ström genom tråden till höger, genom motståndet till höger och ända till slutet. Inga ledningar eller motstånd i en parallellkrets passeras två gånger.
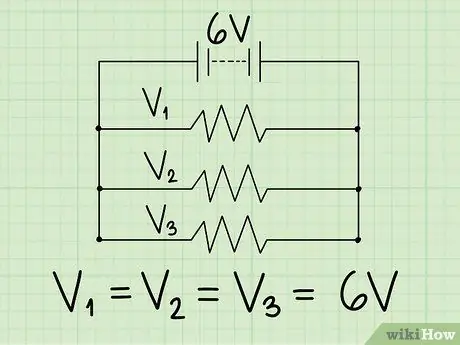
Steg 3. Använd den totala spänningen för att hitta spänningen över varje motstånd
Om du känner till spänningen över hela kretsen är svaret lätt att hitta. Varje parallellkabel har samma spänning som hela den elektriska kretsen. Säg att en elektrisk krets har två motstånd parallellt och ett 6 volt batteri. Hinder är inte särskilt relevanta idag. För att förstå det, kom ihåg seriekretsen som beskrivs ovan:
- Kom ihåg att summan av spänningarna i en seriekrets alltid är lika med den totala spänningen genom den elektriska kretsen.
- Föreställ dig varje väg som strömmen tar i en seriekrets. Detsamma gäller för parallella kretsar: om du lägger till alla spänningar är resultatet lika med den totala spänningen.
- Eftersom strömmen genom varje parallelltråd bara går genom ett motstånd måste spänningen över motståndet vara lika med den totala spänningen.
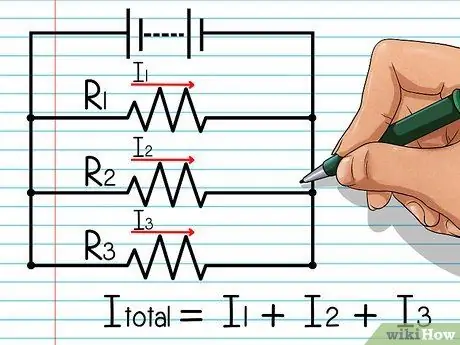
Steg 4. Beräkna den totala strömmen för den elektriska kretsen
Om problemet inte ger den totala spänningen över kretsen måste du slutföra några ytterligare steg. Börja med att hitta den totala strömmen genom den elektriska kretsen. I en parallell krets är den totala strömmen lika med summan av strömmarna genom varje parallell väg.
- Formeln är följande: Itotal = Jag1 + Jag2 + Jag3…
- Om du har svårt att förstå det, tänk dig ett vattenrör som har två grenar. Den totala mängden vatten som flödar i en serie rör är summan av vattnet som flödar i varje rör.
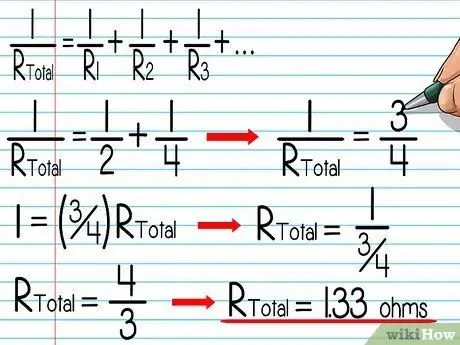
Steg 5. Beräkna det totala motståndet för den elektriska kretsen
Effektiviteten hos ett motstånd reduceras i en parallellkrets eftersom det bara blockerar strömmen genom en tråd. Faktum är att ju fler ledningar i en krets, desto lättare är det för ström att hitta en väg att flyta smidigt. För att hitta det totala motståndet, hitta värdet av R. total i denna ekvation:
- 1 / Rtotal = 1 / R1 + 1 / R2 + 1 / R3 …
- Till exempel har en elektrisk krets resistorer på 2 ohm respektive 4 ohm anslutna parallellt. 1 / Rtotal = 1/2 + 1/4 = 3/4 → 1 = (3/4) Rtotal → Rtotal = 1/(3/4) = 4/3 = ~ 1,33 ohm.
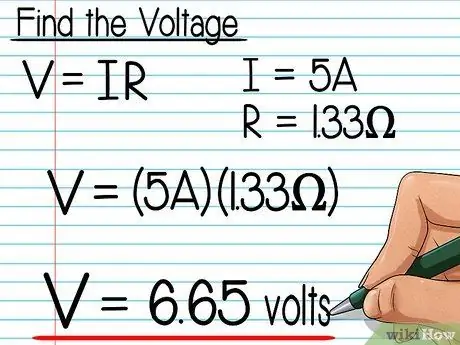
Steg 6. Hitta spänningen från ditt svar
Kom ihåg att när vi hittat den totala spänningen i den elektriska kretsen vet vi redan storleken på spänningen genom varje parallellkabel. Använd Ohms lag för att slutföra beräkningen. Ta en titt på följande exempelfrågor:
- Den elektriska kretsen har en ström på 5 ampere och ett totalt motstånd på 1,33 ohm.
- Enligt Ohms lag är I = V / R så att V = IR
- V = (5A) (1, 33Ω) = 6,65 volt.
Tips
- Om du har en komplicerad elektrisk krets, till exempel med parallellkopplade motstånd och serier, välj de två närmaste motstånden. Hitta det totala motståndet genom de två motstånden med hjälp av reglerna för motstånd i serie och parallella kretsar. Nu kan du behandla det som ett enda motstånd. Fortsätt denna process tills du har en krets där motstånden är anordnade endast i serie eller parallell.
- Spänningen över motståndet kallas ofta "spänningsfallet".
-
Förstå följande termer:
- Elektrisk krets/sträng - Arrangemanget av olika komponenter (motstånd, kondensatorer och induktorer), som är anslutna med kablar och kan få ström.
- Motstånd - ett element som reducerar eller hämmar elektrisk ström.
- Ström - Flödet av elektrisk laddning i kabeln. Uttryckt i Ampere (A).
- Spänning - Mängden elektrisk laddning som passerar varje sekund. Uttryckt i volt (V).
- Motstånd - Ett mått på ett elements motstånd mot elektrisk ström. Uttryckt i ohm (Ω)






