- Författare Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:15.
- Senast ändrad 2025-01-23 12:47.
Förskjutning i fysik betecknar en förändring av objektets position. När du beräknar förskjutning beräknar du hur långt bort ett objekt är baserat på dess initiala och sista platser. Formeln du använder för att beräkna förskjutning beror på variabeln som ges till problemet. Följ dessa steg för att beräkna förskjutning.
Steg
Del 1 av 5: Beräkning av den resulterande förskjutningen

Steg 1. Använd den resulterande förskjutningsformeln om avståndsenheten används för att ange dina start- och slutplatser
Även om avståndet skiljer sig från förskjutning, letar det resulterande förskjutningsproblemet efter hur många kilometer eller meter objektet har färdats. Du kommer att använda denna måttenhet för att beräkna förskjutning och hur långt borta objektets plats avviker från dess utgångspunkt.
- Den resulterande förskjutningsformeln är skriven som: S = x²+y². S är förskjutning. X är objektets första rörelseriktning och Y är objektets andra rörelseriktning. Om ditt objekt bara rör sig i en riktning, då Y = 0.
- Ett objekt kan bara röra sig i högst två riktningar eftersom rörelse längs en nord-/syd- eller öst-/västaxel anses vara neutral rörelse.

Steg 2. Anslut prickarna i rörelseordning och märk dem från A-Ö
Använd en linjal för att rita en rak linje från punkt till punkt.
- Kom också ihåg att ansluta din startpunkt till din slutpunkt med en rak linje. Detta är förskjutningen vi kommer att beräkna.
- Till exempel, om ett objekt rör sig österut 300 m och norrut 400 m, kommer det att bilda en rätt triangel. AB kommer att vara det första benet i triangeln och BC är det andra benet. AC kommer att vara triangelns hypotenusa och dess storlek är föremålets förskjutning. I detta exempel är de två riktningarna öster och norr.

Steg 3. Ange värden för x² och y²
Nu när du känner till objektets två rörelseriktningar anger du värdena i lämpliga variabler.
Till exempel x = 300 och y = 400. Din formel ska se ut så här: S = 300² + 400²
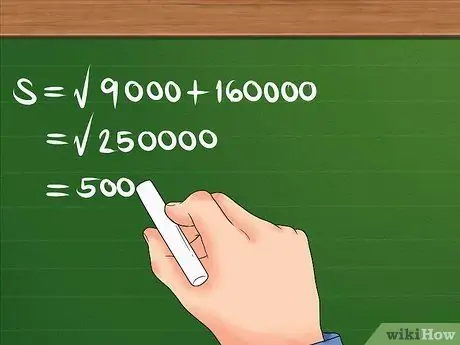
Steg 4. Beräkna formeln med hjälp av ordningen
Fyrkant 300 och 400 först, lägg sedan ihop dem och hitta kvadratroten av summan.
Till exempel: S = 90000 + 160000. S = 250000. S = 500. Nu vet du att förskjutningen är 500 m
Del 2 av 5: När hastighet och tid är kända

Steg 1. Använd den här formeln när problemet berättar ett objekts hastighet och den tid det tar
Vissa matematiska problem kommer inte att berätta hur långt eller hur snabbt ett objekt rör sig. Du kan beräkna förskjutning med den här storleken på tid och hastighet.
-
I detta fall blir formeln: S = 1/2 (u + v) t.
U = objektets initialhastighet, eller hur snabbt objektet börjar röra sig i en viss riktning. V = objektets sluthastighet, eller hur snabbt objektet rör sig mot dess slutliga plats. T = den tid det tar föremålet att nå sin slutliga plats.
- Exempel: En bil kör på vägen i 45 sekunder (tid krävs). Bilen svänger västerut i 20 m/s (initialhastighet) och i slutet av vägen är dess hastighet 23 m/s (slutfart). Beräkna förskjutningen utifrån dessa faktorer.

Steg 2. Ange önskad hastighet och tid i lämpliga variabler
Nu när du vet hur långt bilen rör sig, hur snabbt bilen rör sig i början och slutet kan du hitta avståndet från startplatsen till slutplatsen.
Din formel ska se ut så här: S = 1/2 (20 + 23) 45

Steg 3. Beräkna formeln efter att du har satt värdena på rätt plats
Kom ihåg att följa ordningsföljden, annars kommer förskjutningarna att resultera i mycket olika värden.
- För denna formel spelar det ingen roll om du av misstag byter start- och sluthastighet. Eftersom du först lägger till dessa nummer spelar det ingen roll var de är inom parentes. För andra formler kommer emellertid byte av initial- och sluthastigheter att resultera i olika förskjutningsvärden.
- Din formel ska se ut så här: S = 1/2 (43) 45. Dela först 43 med 2, vilket resulterar i 21, 5. Multiplicera sedan 21, 5 med 45, så resultatet blir 967,5 meter. 967, 5 är storleken på din förskjutning, eller hur långt din bil har flyttat från startpunkten.
Del 3 av 5: När initialhastigheten, accelerationen och tiden är kända
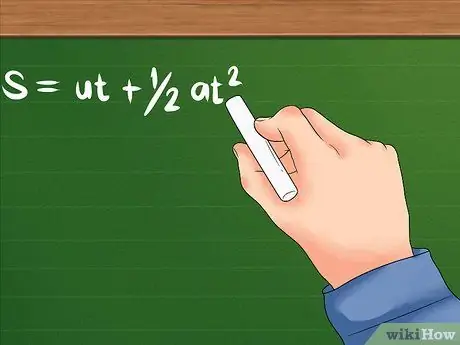
Steg 1. Använd den modifierade formeln när accelerationen är känd utöver initialhastigheten och tiden
Vissa frågor berättar bara hur snabbt objektet rör sig i början, hur snabbt objektet börjar accelerera och hur långt objektet rör sig. Du behöver följande formel.
- Formeln för detta problem är: S = ut + 1/2at². U anger fortfarande initialhastigheten; a är föremålets acceleration, eller hur snabbt dess hastighet börjar förändras. T kan betyda den tid det tar eller en viss tid det tar ett objekt att accelerera. Båda kommer att använda tidsenheter som sekunder, timmar och andra.
- Antag att en bil som rör sig med 25 m/s (initial hastighet) börjar accelerera med 3 m/s2 (acceleration) i 4 sekunder (tid). Vad är förskjutningen av bilen efter 4 sekunder?

Steg 2. Ange värdena i formeln
Till skillnad från den tidigare formeln är endast initialhastigheten representerad här, så se till att ange rätt data.
Baserat på provdata ovan skulle din formel se ut så här: S = 25 (4) + 1/2 (3) 4². Det hjälper till att lägga till parenteser kring din accelerationsstorlek och tid för att hjälpa dig att skilja siffrorna
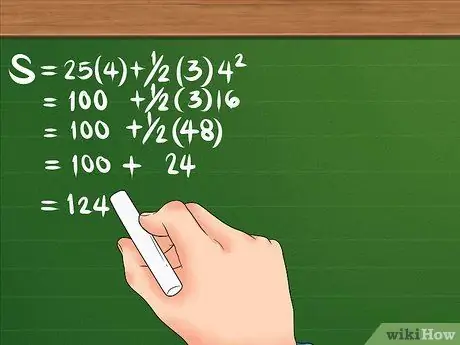
Steg 3. Beräkna förskjutningen genom att göra det i rätt ordningsföljd
Ett snabbt sätt att hjälpa dig att komma ihåg operationssekvensen är åsnebron Kur ir Kua ci Kadang Ba wa Juragan Turtles. Detta representerar rätt ordning: parenteser, rutor, multiplikation, division, addition och subtraktion.
Låt oss titta på formeln igen: S = 25 (4) + 1/2 (3) 4². Först, ruta 4, blir resultatet 16. Därefter multipliceras 16 med 3, vilket gör 48; multiplicera sedan 25 med 4, för att göra 100. Dela 48 med 2, för att göra 24. Din ekvation ska se ut så här: S = 100 + 24. När du lägger ihop de två är förskjutningen 124 meter
Del 4 av 5: Beräkning av vinkelförskjutning

Steg 1. Hitta vinkelförskjutningen när objektet rör sig i en cirkulär bana
Även om du fortfarande kommer att beräkna förskjutning med en rak linje, måste du hitta skillnaden mellan objektets start- och slutplatser när det rör sig i en cirkulär bana.
- Föreställ dig en tjej som sitter på en mery-go-round. När han snurrar med karusellen kommer han att röra sig i en cirkulär bana. Vinkelförskjutning försöker hitta det kortaste avståndet mellan de initiala och sista platserna när objektet inte rör sig i en rak linje.
- Formeln för vinkelförskjutning är: = S/r, där S är den linjära förskjutningen, r är radien och är vinkelförskjutningen. Linjär förskjutning är hur långt ett föremål rör sig längs en båge. Radien är objektets avstånd till cirkelns mitt. Vinkelförskjutning är det värde vi vill hitta.

Steg 2. Anslut den linjära förskjutningen och radien till ekvationen
Kom ihåg att radien är avståndet från cirkelns mitt; vissa problem kommer att berätta diametern på en cirkel, som måste divideras med 2 för att hitta radien.
- Här är ett exempelproblem: En tjej åker på en mery-go-round. Sätet är 1 meter från cirkelns mitt (radien). Om tjejen rör sig i en bågbana 1,5 meter (linjär förskjutning), vad är hennes vinkelförskjutning?
- Din ekvation kommer att se ut så här: = 1,5/1.
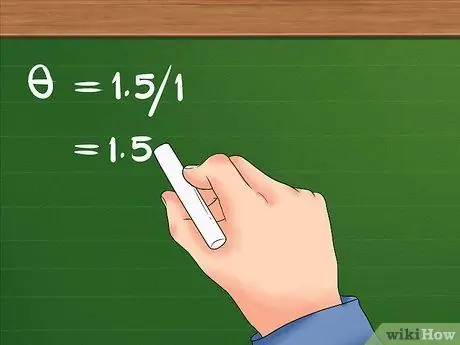
Steg 3. Dela den linjära förskjutningen med radien
Denna uppdelning kommer att resultera i vinkelförskjutning av föremålet.
- Efter att ha delat 1,5 med 1 blir resultatet 1,5 Flickans vinkelförskjutning är 1,5 radianer.
- Eftersom vinkelförskjutning mäter hur mycket ett föremål roterar från sitt utgångsläge, bör det mätas som en vinkel, inte ett avstånd. Radian är den enhet som används för att mäta vinklar.
Del 5 av 5: Förståelse om migration
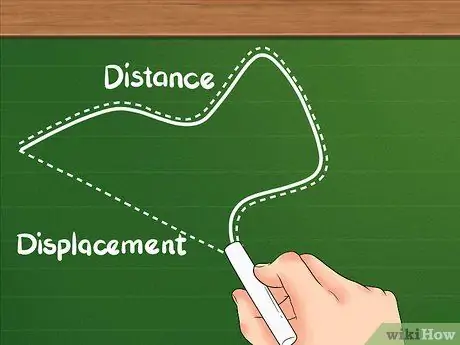
Steg 1. Vet att avstånd har en annan definition än förskjutning
Avstånd visar hur långt det totala avståndet rest av objektet.
- Avstånd är ofta känt som en skalär kvantitet. Avståndet visar avståndet för ett objekt oberoende av objektets riktning.
- Till exempel, om du går 2 steg österut, 2 steg söderut, 2 steg västerut och sedan 2 steg norrut, kommer du tillbaka till ditt utgångsläge. Trots att du har gått igenom summan distans 10 steg bort, du bara flytta 0 steg bort eftersom din slutliga plats är densamma som din startplats (din väg liknar en ruta).

Steg 2. Förstå att förskjutning är skillnaden mellan två platser
Förskjutning är inte den totala summan av rörelse som avstånd; skift fokuserar på området mellan dina start- och slutplatser.
- Förskjutning kallas en vektormängd och visar förändringen i objektets position genom att beakta objektets rörelseriktning.
- Till exempel går du österut i 5 steg. Om du går tillbaka 5 västerut kommer du att röra dig i motsatt riktning från din ursprungliga plats. Även om du har täckt 10 steg har din position inte ändrats; din förskjutning är 0 steg.

Steg 3. Kom ihåg orden framåt och bakåt när du försöker föreställa dig förskjutning
Att röra sig i motsatt riktning eliminerar förskjutningen av ett objekt.
Tänk dig en fotbollstränare fram och tillbaka på sidan. När han ropade på spelarna skiftade han från vänster till höger flera gånger. Om du tittar på honom när han rör sig från vänster till höger, observerar du den totala sträckan han har rest. Antag dock att tränaren stannar för att prata med quarterbacken på sidlinjen. Om han befinner sig på en annan punkt än sin ursprungliga plats innan han flyttar, observerar du tränarens rörelse

Steg 4. Vet att förskjutning mäts med en rak väg, inte en cirkelbana
För att hitta förskjutning måste du hitta det kortaste och mest effektiva sättet att beräkna skillnaden mellan två punkter.
- En cirkulär väg tar dig från din startplats till din slutliga plats, men det är inte den kortaste vägen. För att hjälpa dig att visualisera det, föreställ dig att du går i en rak linje och stöter på en pelare. Du kan inte bryta igenom den här pelaren, så du går runt den. Även om din slutliga position är densamma som om du bröt igenom pelaren, behöver du extra steg för att nå det målet.
- Även om förskjutning representerar en rak väg, vet du att du kan mäta förskjutningen av ett objekt för närvarande rör sig i en cirkulär bana. Denna förskjutning kallas vinkelförskjutning och kan beräknas genom att hitta den kortaste vägen från den ursprungliga platsen till den slutliga platsen.

Steg 5. Vet att förskjutning kan vara negativ, till skillnad från avstånd
Om din slutliga plats nås genom att röra dig i motsatt riktning mot din ursprungliga riktning, är din förskjutning negativ.
- Till exempel går vi 5 steg österut och sedan 3 steg västerut. Även om du genom beräkning flyttar 2 steg från din startplats, är din förskjutning -2 eftersom du rör dig i motsatt riktning. Ditt avstånd kommer alltid att vara positivt eftersom du inte kan räkna bakåt i steg, kilometer osv.
- Negativ förskjutning betyder inte att förskjutningen minskar. Negativ betyder bara att riktningen är motsatt.

Steg 6. Inse att avstånd och förskjutning ibland kan vara desamma
Om du går rakt i 25 steg och stannar är avståndet du reser lika med förskjutningen från din ursprungliga plats.
- Detta gäller bara när du flyttar från en plats från din startplats i en rak linje. Till exempel bor du i San Francisco, Kalifornien, och får ett nytt jobb i Las Vegas, Nevada. Du måste flytta till Las Vegas för att vara nära ditt jobb. Om du sätter dig på ett flygplan som flyger hetero från San Francisco till Las Vegas kommer du att resa samma sträcka och förskjutning x.
- Men om du kör från San Francisco till Las Vegas kommer du att resa en sträcka x, men åka en sträcka y. Eftersom bilkörning vanligtvis har varierande riktningar (öster om denna väg, väster om den vägen), reser du längre sträckor än det kortaste avståndet mellan de två städerna.






