- Författare Jason Gerald [email protected].
- Public 2024-01-15 08:24.
- Senast ändrad 2025-01-23 12:48.
P -värdet är ett statistiskt mått som hjälper forskare att avgöra om deras hypotes är korrekt. P -värdet används för att avgöra om resultaten av deras experiment ligger inom de värden som är normala för de studerade sakerna. Vanligtvis, om P -värdet för en datamängd faller under ett visst förutbestämt värde (till exempel 0,05), kommer forskare att avvisa nollhypotesen i sitt experiment - med andra ord kommer de att utesluta en hypotes där experimentvariabeln har ingen signifikant effekt på resultatet. Idag finns p -värden vanligtvis i referenstabeller genom att beräkna värdet för chi -kvadrat.
Steg

Steg 1. Bestäm de förväntade resultaten av ditt experiment
Vanligtvis, när forskare utför ett experiment och undersöker resultaten, har de redan en uppfattning om de normala eller vanliga resultaten i förväg. Detta kan baseras på resultaten från tidigare experiment, tillförlitliga observationsdatauppsättningar, vetenskaplig litteratur och/eller andra källor. Bestäm ditt förväntade resultat för ditt experiment och skriv ner det som ett tal.
Exempel: Antag att en tidigare studie visade att på nationell nivå utfärdades hastighetsbiljetter oftare till röda bilar än till blå bilar. Antag att genomsnittsresultatet på nationell nivå visar ett förhållande på 2: 1 och förhållandet mellan röda bilar är mer. Vi vill ta reda på om polisen i vår stad också får samma tendens genom att analysera hastighetsbiljetten som utfärdats av polisen i vår stad. Om vi tog ett slumpmässigt urval av 150 fartbiljetter till både röda och blå bilar i vår stad, skulle vi förvänta oss 100 för röd bil och 50 för blå bilar om polisenheten i vår stad ger en biljett enligt jämförelsen på nationell nivå.

Steg 2. Bestäm dina experimentella observationer
Nu när du har bestämt ditt förväntade värde kan du köra ditt experiment och hitta det sanna värdet (eller observationen). Skriv igen resultatet som ett tal. Om vi manipulerar några experimentella förhållanden och de observerade resultaten skiljer sig från de förväntade resultaten, finns det två möjligheter: antingen hände detta av en slump, eller så var det vår manipulation av de experimentella variablerna som orsakade denna skillnad. Syftet med att hitta p-värdet är i grunden att avgöra om de observerade resultaten skiljer sig från de förväntade resultaten till en punkt där nollhypotesen-hypotesen att det inte finns något samband mellan experimentvariabeln och de observerade resultaten-inte kan avvisas.
Exempel: Antag att vi i vår stad slumpmässigt väljer ut 150 hastighetsbiljetter som tilldelas både röda och blå bilar. Vi får 90 en biljett till en röd bil och 60 för den blå bilen. Detta skiljer sig från det resultat vi förväntade oss, dvs. 100 och 50. Hade vår experimentella manipulation (i det här fallet byte av datakälla från nationell till lokal) någon förändring i resultaten, eller hade vår stadspolis samma tendenser som nationell nivå, och vi såg bara tillfälligheter? P -värdet hjälper oss att bestämma det.

Steg 3. Bestäm frihetsgraderna för ditt experiment
Frihetsgraderna är ett mått på mängden variation i studien, som bestäms av antalet kategorier du undersöker. Ekvationen för frihetsgraderna är Frihetsgrader = n-1, där n är antalet kategorier eller variabler som analyseras i ditt experiment.
-
Exempel: Vårt experiment har två kategorier av resultat: en för den röda bilen och en för den blå bilen. Således har vi i vårt experiment 2-1 = 1 grad av frihet.
Om vi jämför röda, blåa och gröna bilar kommer vi att ha
Steg 2. grader av frihet och så vidare.

Steg 4. Jämför de förväntade resultaten med de observerade resultaten med chi -kvadrat
Chi i kvadrat (skrivet x2) är ett numeriskt värde som mäter skillnaden mellan de förväntade och observerade värdena från experimentet. Ekvationen för chi i kvadrat är: x2 = ((o-e)2/e), där o är det observerade värdet och e är det förväntade värdet. Lägg ihop resultaten från denna ekvation för alla möjliga utfall (se nedan).
- Observera att denna ekvation använder operatoren (sigma). Med andra ord måste du beräkna ((| o-e | -.05)2/e) för varje möjligt utfall, lägg sedan ihop resultaten för att få värdet för chi -kvadrat. I vårt exempel har vi två resultat - en bil som får en röd eller en blå biljett. Således kan vi beräkna ((o-e)2/e) två gånger - en gång för den röda bilen och en gång för den blå bilen.
-
Exempel: Låt oss ansluta våra förväntade värden och observationer till ekvationen x2 = ((o-e)2/e). Kom ihåg att på grund av sigma-operatören måste vi beräkna ((o-e)2/e) två gånger - en gång för den röda bilen och en gång för den blå bilen. Behandlingsstegen är följande:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Steg 5. Välj en betydelse
Nu när vi känner till vårt experimentella kit frihetsgrader och chi-kvadratvärdet, är det bara en sista sak vi behöver göra innan vi kan hitta vårt p-värde-vi måste bestämma nivån av betydelse. I grund och botten är signifikansnivå ett mått på hur säkra vi är på våra resultat - en låg nivå av betydelse motsvarar en låg sannolikhet att resultatet av ett experiment berodde på slump och vice versa. Nivån av signifikans skrivs som en decimal (t.ex. 0,01), vilket motsvarar den procentuella chansen att resultatet av experimentet berodde på slumpen (i detta fall 1%).
- Enligt konvention sätter forskare vanligtvis ett signifikansvärde för sina experiment på 0,05 eller 5 procent. Detta innebär att experimentella resultat som motsvarar denna signifikansnivå har högst 5% chans att slumpmässigt. Med andra ord finns det en 95% chans att resultaten beror på att forskaren manipulerar de experimentella variablerna och inte slumpen. För de flesta experiment anses 95% förtroende för förhållandet mellan de två variablerna ha varit framgångsrika för att visa sambandet mellan de två.
- Exempel: För vårt röda och blåa bilexempel, låt oss följa det vetenskapliga avtalet och bestämma vår betydelse 0, 05.
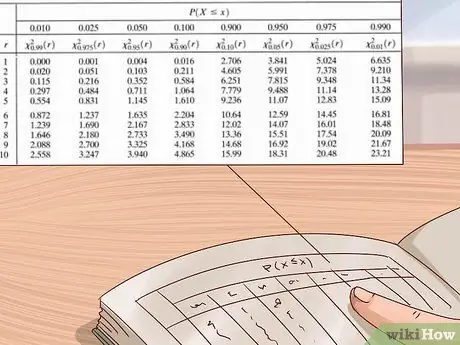
Steg 6. Använd chi square distributionstabellen för att uppskatta ditt p-värde
Forskare och statistiker använder stora värdetabeller för att beräkna p -värden för sina experiment. Denna tabell är vanligtvis skriven med den vertikala axeln till vänster som visar frihetsgraderna och den horisontella axeln på toppen visar p-värdena. Använd den här tabellen genom att först hitta dina frihetsgrader och sedan läsa raderna från vänster till höger tills du hittar det första värdet som är större än ditt chi -kvadratvärde. Titta på p-värdet högst upp i kolumnen-ditt p-värde ligger mellan detta värde och det näst största värdet (det högra värdet är till vänster om det).
- Chi -kvadratiska distributionstabeller finns tillgängliga från en mängd olika källor - de kan enkelt hittas online eller i vetenskapliga eller statistiska läroböcker. Om du inte har en, använd tabellen som visas på bilden ovan eller ett gratis onlinebord, till exempel det som tillhandahålls av medcalc.org här.
-
Exempel: Vår chi i kvadrat är 3. Så låt oss använda chi square-fördelningstabellen på bilden ovan för att hitta ett ungefärligt p-värde. Eftersom vi vet att vårt experiment bara har
Steg 1. frihetsgrader utgår vi från det översta bordet. Vi går från vänster till höger i den här raden tills vi hittar ett värde högre än
Steg 3. - vårt chi -kvadratvärde. Det första värdet vi hittar är 3,84. Om vi tittar upp den här kolumnen ser vi att motsvarande p-värde är 0,05. Det betyder att vårt p-värde är mellan 0,05 och 0,1 (näst största p-värde i tabellen).

Steg 7. Bestäm om du vill avvisa eller försvara din nollhypotes
Eftersom du har hittat ett ungefärligt p-värde för ditt experiment kan du bestämma om du vill avvisa experimentets nollhypotes eller inte (som en påminnelse är detta hypotesen att den experimentella variabeln du manipulerade inte hade någon effekt på resultaten du observerade). Om ditt p-värde är lägre än ditt signifikansvärde, grattis-du har bevisat att det finns stor sannolikhet för att det finns ett samband mellan de variabler du manipulerade och dina observationer. Om ditt p-värde är större än ditt signifikansvärde kan du inte med säkerhet säga att resultaten du observerar är resultatet av en ren tillfällighet eller manipulation av ditt experiment.
- Exempel: Vårt p-värde ligger mellan 0,05 och 0,1. Det vill säga att det inte är mindre än 0,05, så tyvärr har vi kan inte förkasta vår nollhypotes. Detta innebär att vi inte når den lägsta 95% konfidensgräns som vi har satt så att det kan sägas att polisen i vår stad ger biljettbiljetter till röda och blå bilar i ett förhållande som skiljer sig ganska mycket från riksgenomsnittet.
- Med andra ord finns det en 5-10% chans att våra observationer inte är resultatet av en platsändring (analyserar vår stad, och inte hela delen), utan är tillfälligheter. Eftersom vi letar efter en sannolikhet på mindre än 5%kan vi inte säga att vi övertygad att polisen i vår stad tenderar att biljetter röda bilar - det finns en liten men statistiskt mycket annorlunda möjlighet att de inte har denna tendens.
Tips
- En vetenskaplig miniräknare kommer att göra beräkningarna mycket enklare. Du kan också söka efter miniräknare online.
- Du kan beräkna p-värden med hjälp av flera datorprogram, inklusive vanligt förekommande kalkylprogram och mer specialiserad statistisk programvara.






