- Författare Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:24.
- Senast ändrad 2025-01-23 12:47.
Inom maskinteknik är utväxlingsförhållandet en direkt mätning av rotationshastigheten för två eller flera växlar som är konkurrenskraftiga. Som en allmän regel när det gäller två växlar, om drivhjulet (växeln som mottar roterande kraft direkt från motorn, motorn, etc.) är större än det drivna kugghjulet, kommer det drivna kugghjulet att rotera snabbare och vice versa. Vi kan skriva detta grundläggande koncept i en formel Utväxling = T2/T1, T1 är antalet tänder i den första växeln och T2 är antalet tänder i den andra växeln.
Steg
Metod 1 av 2: Beräkning av utväxlingsförhållande i växelkrets
Två växlar
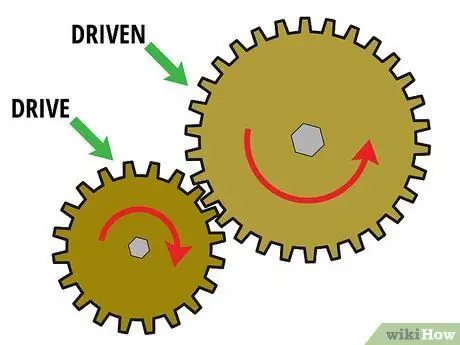
Steg 1. Börja med en tvåväxlad uppsättning
För att bestämma utväxlingen måste du ha minst två växlar förreglade. Dessa två sammankopplade kugghjul kallas "växelsatser". I allmänhet är den första växeln en "drivväxel" monterad på motoraxeln och den andra växeln är en "driven växel" monterad på lastaxeln. Ett antal kugghjul kan också finnas mellan för att överföra kraft från drivhjulet till det drivna kugghjulet. Dessa växlar kallas "obelastade växlar".
Låt oss nu titta på en växelsats som bara har två växlar i den. För att beräkna utväxlingen måste dessa två växlar interagera med varandra. Med andra ord måste tänderna meshas och den ena måste rotera den andra. Anta till exempel att du har en liten drivväxel (växel 1) som roterar en större driven växel (växel 2)
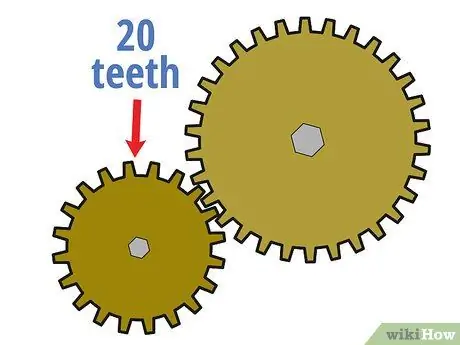
Steg 2. Räkna antalet tänder på drivhjulet
Ett sätt att beräkna utväxlingsförhållandet mellan två sammankopplade växlar är att jämföra antalet tänder (små tandliknande stötar på hjulkanten) de har. Börja med att räkna hur många tänder som finns i drivväxeln. Du kan göra detta genom att beräkna manuellt eller ibland genom att titta på informationen som skrivs ut på drivhjulet.
Anta till exempel att det mindre drivhjulet i systemet har 20 tänder.
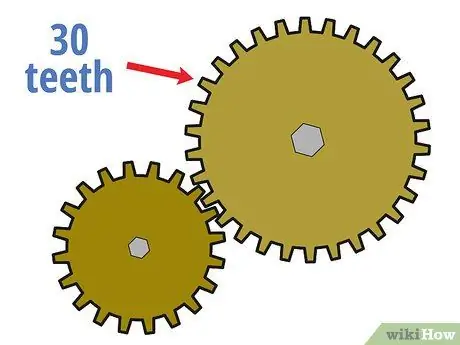
Steg 3. Räkna antalet tänder på den drivna växeln
Räkna sedan hur många tänder det finns i den drivna växeln som du gjorde tidigare för drivväxeln.
Anta till exempel att den drivna växeln har 30 tänder.
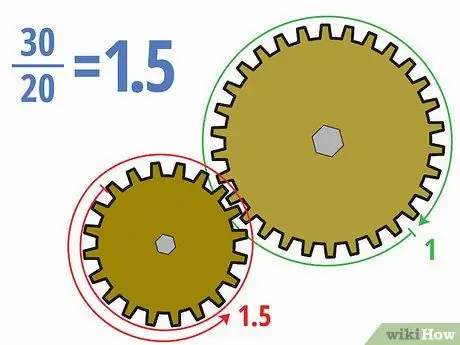
Steg 4. Dela antalet tänder med varandra
Nu när du vet hur många tänder som finns i varje växel kan du ganska enkelt beräkna utväxlingen. Dela tänderna på det drivna kugghjulet med tänderna på drivhjulet. Du kan skriva svaret i decimal-, bråk- eller förhållandeform (som x: y) beroende på din uppgift.
- I exemplet ovan ger 30/20 = att dela 30 tänder i den drivna växeln med 20 tänder i drivhjulet 1, 5. Vi kan också skriva in det 3/2 eller 1, 5: 1.
- Innebörden med detta utväxlingsförhållande är att det mindre drivhjulet måste rotera en och en halv gång för att det större drivna redskapet ska göra ett komplett varv. Eftersom den drivna växeln är större kommer den drivna växeln att rotera långsammare.
Mer än två växlar
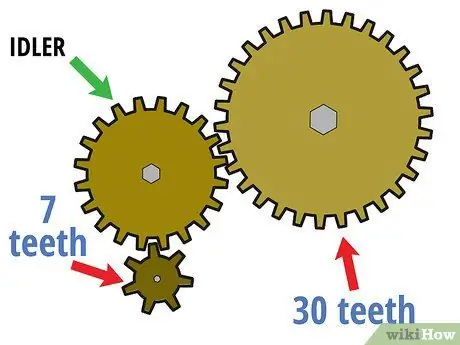
Steg 1. Börja med en växelsats som har mer än två växlar
Som namnet antyder kan en "växelsats" bestå av en lång serie växlar, inte bara en drivväxel och en driven växel. I det här fallet förblir den första växeln drivväxeln, den sista växeln förblir den drivna växeln och mellanväxeln blir "tomgångsväxeln". Dessa olastade kugghjul används ofta för att ändra rotationsriktning eller för att ansluta två växlar när direkt växeljustering skulle göra dem tunga eller otillgängliga.
Anta till exempel att den tvåväxlade kretsen som beskrivs ovan nu drivs av en kugghjul som har sju små tänder. I det här fallet blev kugghjulet som hade 30 fasta tänder det drivna kugghjulet och drevet som hade 20 tänder (som tidigare var drivenheten) är nu det lossade redskapet
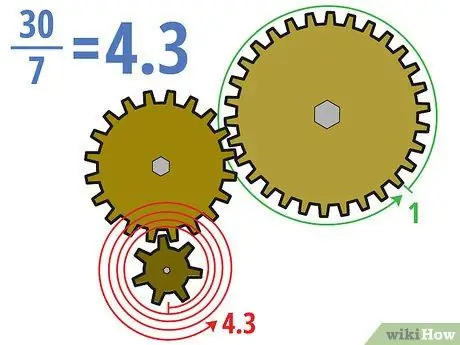
Steg 2. Dela upp antalet kuggar på drivhjulet och det drivna kugghjulet
Det viktiga att komma ihåg vid hantering av växlar som har mer än två växlar är att endast drivväxeln och det drivna växeln (vanligtvis första och sista växeln) är viktiga. Med andra ord påverkar obelastade växlar inte alls växelförhållandet för hela setet. När du väl har identifierat drivväxeln och drivväxeln kan du beräkna växelkvoten på samma sätt som tidigare.
I exemplet ovan kommer vi att beräkna utväxlingsförhållandet genom att dividera de trettio tänderna på det drivna drevet med de sju tänderna på det nya drivhjulet. 30/7 = ca. 4, 3 (eller 4, 3: 1). Detta innebär att drivhjulet måste rotera cirka 4,3 gånger för att det mycket större drivna kan växla en gång.
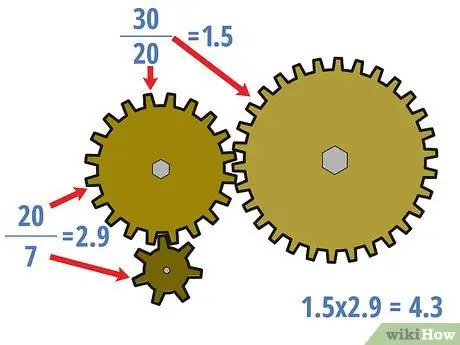
Steg 3. Beräkna vid behov utväxlingsförhållandet för mittväxeln
Du kan beräkna utväxlingsförhållanden som också innefattar olastade växlar, och du kanske vill göra det i vissa situationer. Börja i det här fallet vid drivväxeln och arbeta dig upp till lastväxeln. Behandla den tidigare växeln som en drivväxel hela vägen till nästa växel. Dela antalet tänder på varje "driven" växel med antalet tänder på "driv" -växeln för varje uppsättning låsande kugghjul för att beräkna mittväxeln.
- I exemplet ovan är mittväxeln 20/7 = 2, 9 och 30/20 = 1, 5. Det bör noteras att dessa förhållanden inte är desamma som utväxlingen för hela uppsättningen, vilket är 4,3.
- dock, det bör också noteras att (20/7) × (30/20) = 4, 3. I allmänhet bör förhållandena för mittväxlarna i växelsatsen multipliceras till lika med förhållandet för alla växlar.
Metod 2 av 2: Beräkning av förhållande/hastighet
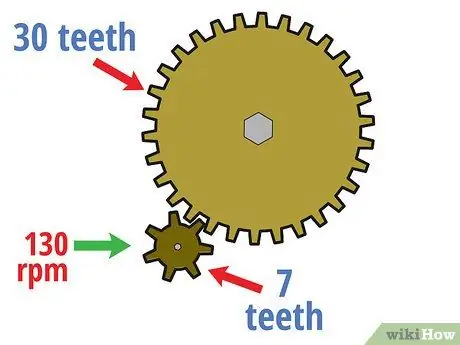
Steg 1. Beräkna rotationshastigheten för drivhjulet
Med hjälp av konceptet utväxlingsförhållanden är det lätt att avgöra hur snabbt det drivna kugghjulet roterar baserat på drivningens "ingångshastighet". Till att börja med, beräkna rotationshastigheten för drivhjulet. I många växelberäkningar resulterar detta i varv per minut (rpm), även om andra hastighetsenheter också kan användas.
Anta till exempel i exemplet med växelkretsen ovan med ett drivhjul med sju tänder och ett drivat kugghjul med 30 tänder, roterar drivhjulet med en hastighet av 130 varv / min. Med denna information kommer vi att beräkna hastigheten på den drivna växeln i följande steg
Steg 2. Anslut denna information till formeln S1 × T1 = S2 × T2
I denna formel avser S1 drivhjulets rotationshastighet, T1 hänvisar till drivhjulets tänder och S2 och T2 hänvisar till hastigheten och tänderna hos det drivna kugghjulet. Fyll i dessa variabler tills du bara har en variabel kvar.
- Ofta i frågor som denna hittar du storleken på S2, även om det är möjligt att hitta andra variabler. I exemplet ovan får du följande information:
- 130 varv / min × 7 = S2 × 30
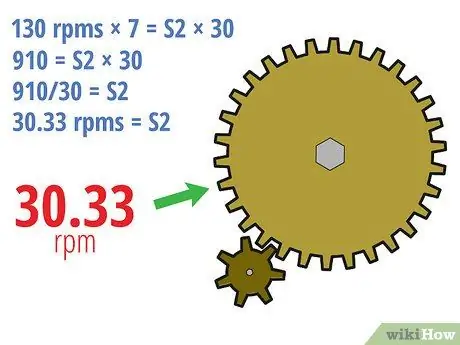
Steg 3. Slutför
Att beräkna de återstående variablerna är bara ett grundläggande matematikproblem. Förenkla de återstående ekvationerna och isolera variabeln på ena sidan av ekvationstecknet så får du svaret. Glöm inte att skriva det i rätt enheter. Du kan förlora värde från läxor på grund av detta.
- I exemplet ovan kan vi lösa detta genom att:
- 130 varv / min × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30, 33 varv / min = S2
- Med andra ord, om drivhjulet roterar med en hastighet av 130 varv / min, kommer det drivna kugghjulet att rotera med en hastighet av 30,33 varv / minut. Eftersom den drivna växeln är mycket större kommer den drivna växeln att rotera mycket långsammare.
Tips
- För att se hur principen för utväxlingsförhållande gäller, prova att cykla. Observera att det enklaste sättet att klättra är när du har en liten växel fram och en stor växel bak. Det är lättare att vända den mindre växeln med kraften i pedalerna, men det tar många varv för bakhjulet att vända jämfört med växelinställningen du skulle använda för plana ytor. Detta gör att du rör dig långsammare.
- Ett nedgraderat system (när belastningsvarvtalet är lägre än motorvarvtalet) kommer att kräva en motor som ger optimal effekt vid högre rotationshastigheter.
- Effekten som krävs för att driva lasten höjs eller sänks från motorn genom utväxlingen. Denna motor måste bytas ut för att ge den effekt som belastningen kräver efter att utväxlingsförhållandet har beräknats. Ett upphöjt system (när belastningsvarvtalet är större än motorvarvtalet) kommer att kräva en motor som ger optimal effekt vid lägre rotationshastigheter.






