- Författare Jason Gerald [email protected].
- Public 2024-01-19 22:14.
- Senast ändrad 2025-01-23 12:47.
Platsvärde, eller begreppet att värdet på ett tal (0-9) bestäms av dess position i ett visst tal, är ett grundläggande begrepp i matematik. Eftersom detta koncept är så enkelt för människor som redan förstår det, kan det vara ganska komplicerat att lära ut det. Men när eleverna har förstått detta koncept kommer de att vara redo och glada att använda sina nya färdigheter och lära sig mer komplexa matematiska begrepp.
Steg
Del 1 av 3: Introduktion till de grundläggande begreppen

Steg 1. Ta dig tid att lära ut platsvärde
Om du undervisar inom en fördefinierad läroplan bör du redan ha en uppfattning om hur platsvärde ska passa in i ett bredare lärande. Om du undervisar eller undervisar hemma blir lärandestrukturen mer flexibel. Planera att lära ut platsvärde någon gång efter att eleverna har lärt sig att räkna och utföra enkla additions- och subtraktionsoperationer - vanligtvis runt årskurs 1 eller årskurs 2. En förståelse av platsvärde kommer att utgöra en grund för dessa barn att förstå mer komplexa matematiska begrepp.

Steg 2. Presentera konceptet att räkna grupper av siffror
De flesta av barnens elever lär sig bara räkna siffror en efter en: en … två … tre … fyra. Detta är tillräckligt för grundläggande addition och subtraktion, men fortfarande för enkelt för att ge en solid grund för att förstå mer komplexa funktioner. Innan du lär dem hur man bryter ner stora siffror till sina respektive platsvärden är det en bra idé att lära dem att dela upp en grupp små siffror i stora siffror.
- Lär dina elever att räkna två två, tre tre, fem fem och tio tio. Detta är ett grundläggande koncept för eleverna att förstå innan de lär sig om platsvärde.
- Försök i synnerhet att bygga upp en stark "spänning i tiotal". Modern matematik använder siffran tio som bas, vilket gör det lättare för barn att lära sig mer komplexa system om de vänjer sig vid att tänka på detta sätt. Lär dina elever att instinktivt gruppera siffror i uppsättningar om tio.

Steg 3. Granska begreppet platsvärde
Uppdatera din förståelse. Se till att du helt förstår detta koncept själv innan du försöker lära det till en grupp unga studenter. Enkelt uttryckt är platsvärdet tanken att värdet på ett tal (0-9) beror på dess "plats" eller position i ett tal.

Steg 4. Förklara skillnaden mellan siffror och siffror
Tal är symboler för de tio grundnumren som utgör alla nummer: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Dessa nummer kombineras för att bilda alla andra nummer. Ett tal kan vara ett tal (t.ex. talet 7), men bara om det inte är grupperat med andra nummer. När två eller flera nummer är grupperade bildar sekvensen av talen det större talet.
Visa att "1" i sig är nummer ett och "7" är siffran sju. När de grupperas som "17" bildar de två siffrorna talet sjutton. På samma sätt bildar "3" och "5" tillsammans talet trettiofem. Visa några andra exempel så att eleverna kan gå hemförståelse
Del 2 av 3: Undervisning med visuella exempel
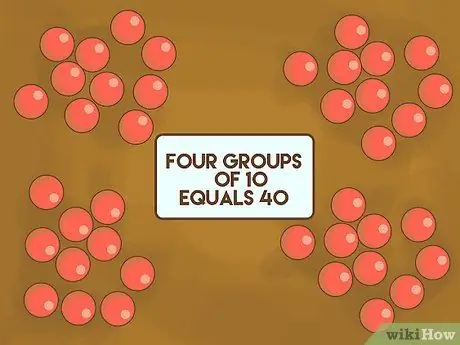
Steg 1. Visa barnen att det är lättare att räkna tio till tio
Använd 30-40 objekt som är små, räknade och ganska homogena. Till exempel: stenar, marmor eller ett suddgummi. Sprid ut det på bordet framför eleverna. Förklara att i modern matematik använder vi talet 10 som grund. Ordna objekten i flera grupper och räkna sedan dem framför klassen. Visa dem att fyra grupper om 10 småstenar är lika med 40.

Steg 2. Översätt exemplet med småsten till skrivna nummer
Skriv konceptskissen på tavlan. Skapa först ett vanligt T-diagram. Skriv siffran 1 i det övre högra hörnet av T -diagrammet. Skriv sedan siffran 10 längst upp till vänster. Skriv ett 0 i kolumnen till höger märkt "1" och skriv en 4 i kolumnen till vänster märkt "10". Nu kan du förklara för klassen att varje nummer som görs med småsten har sin egen "plats".
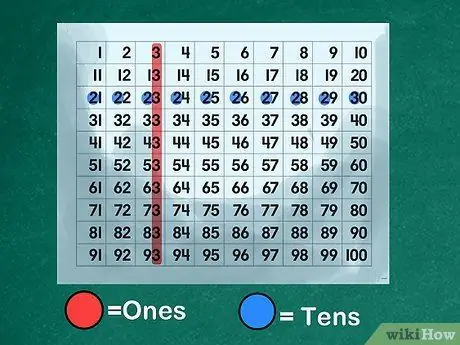
Steg 3. Använd en sifferknapp för att illustrera platsvärdesunderlaget
Skapa eller skriv ut en "nummerplatta" som visar alla siffror i ordning från 1 till 100. Visa eleverna hur siffrorna 0 till 9 interagerar med siffrorna 10 till 100. Förklara att varje nummer från 10 till 99 består av två siffror, en ett nummer på "enorna" och ett annat nummer på "tio" platsen. Visa att siffran "4" representerar "fyra" när den är på "enorna", men fungerar som ett prefix för talet "40" när den är på "tio" -platsen.
- Illustrera platsen för "enheter". Rikta klassen att namnge alla siffror som har siffran "3" på platsen "enor": 3, 13, 23, 33, 43, 53, 63, 73, 83, 93.
- Förklara om "tiotalet". Instruera eleverna att ange alla siffror som har ett "2" istället för "tior": 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Förklara att "3" i "23" är staplad ovanpå "20" markerad med siffran "2." Lär dina barn att läsa platsen "tiotal" som en utlösande faktor för lärande.

Steg 4. Experimentera med andra visuella undervisningsverktyg
Du kan ordna fysiska föremål eller rita dem på tavlan. Du kan förklara platsvärdet genom att använda steg av monetärt värde, som eleverna kanske redan har studerat, för att relatera dem till skalade numeriska värden. För en rolig och interaktiv aktivitet, försök använda eleverna själva som ett "grupp" -värde.
Mänskligt minne domineras av visuella saker, så begreppet platsvärde är fortfarande abstrakt tills du kan göra det visuellt. Samtidigt kan numeriska symboler själva fortfarande vara abstrakta för barn! Leta efter sätt att rama in gruppräkning och placera värdeaktiviteter så att de är enkla, konkreta och intuitiva
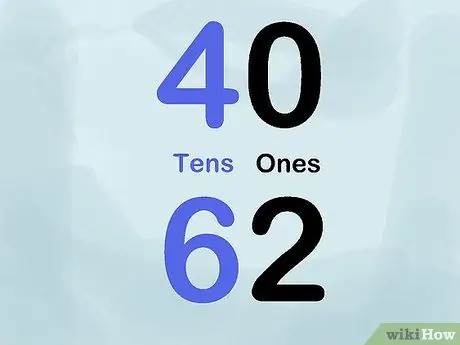
Steg 5. Använd färg
Försök att använda krita eller markörer med olika färg för att visa platsvärdet. Skriv till exempel olika siffror med en svart markör för "enorna" och en blå markör för "tio". Således skriver du 40 med siffran "4" i blått och talet "0" i svart. Upprepa detta trick för ett stort antal nummer för att visa tillämpningen av platsvärde på tavlan.
Del 3 av 3: Använd interaktiva exempel
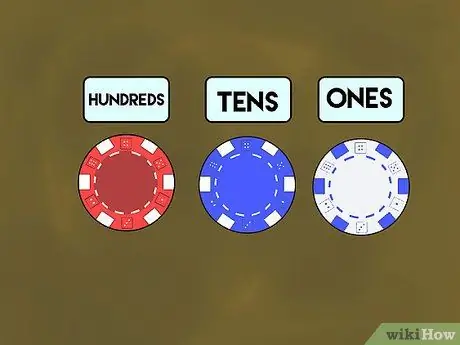
Steg 1. Undervisa med pokerchips
Fördela först pokermarkerna till varje elev. Berätta för dem att de vita marker representerar "enorna" -platsen, de blå marker för "tiotal" och de röda markerna representerar "hundratals". Visa sedan dina elever hur man gör siffror med hjälp av platsvärden i form av färgglada marker. Namnge ett nummer (säg 7) och placera det vita chipet till höger om ditt skrivbord.
- Namnge ett annat nummer - till exempel 30. Sätt tre blå marker som representerar 3 (på "tio" -platsen) och noll vita marker för att representera 0 (på "enorna" -platsen).
- Du behöver inte använda pokerchips. Du kan använda vilket objekt som helst för att representera de tre grundläggande "plats" -värdena så länge varje grupp (chipfärg, etc.) är standard, homogen och lätt igenkännlig.

Steg 2. Instruera eleverna att utbyta bitar med varandra
Denna metod kan illustrera de låga platsvärdena som utgör de högre platsvärdena. När eleverna har visat en god förståelse för platsvärde, lär du din klass hur man byter vita "ena" marker mot blå "tio" marker och byter sedan "tio" marker mot "hundratals". Fråga eleverna, "Hur många blå marker får jag genom att byta ut 16 vita marker? Om jag byter ut tre blå marker, hur många vita marker får jag?"

Steg 3. Visa hur du gör addition och subtraktion med pokerchips
Detta koncept kan bara läras ut efter att eleverna har behärskat utbytet av pokerchips. Det är bra att börja med att skriva ett exempel.
- För det grundläggande tilläggsproblemet, be eleverna lägga ner tre blå marker (tior) och sex vita marker (enor). Fråga eleverna om siffrorna som bildas med chipsen. (Svaret är 36!)
- Fortsätt arbeta med samma nummer. Låt dina elever lägga till fem vita marker till siffran 36. Fråga dem om det aktuella numret. (Svaret är 41!) Ta sedan ett blått chip och fråga dem det aktuella numret. (Svaret är 31!)






