Det ömsesidiga eller ömsesidiga är mycket användbart i alla typer av algebraiska ekvationer. Till exempel, när du delar en fraktion med en annan, multiplicerar du den första fraktionen med den ömsesidiga av den andra. Du måste också använda inversen när du letar efter ekvationen för en linje.
Steg
Metod 1 av 3: Hitta inversen av en bråkdel eller heltal
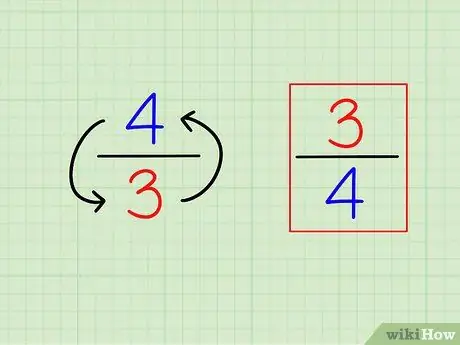
Steg 1. Hitta ömsesidigheten för fraktionen genom att vända den
Definitionen av "ömsesidig" eller motsatsen är mycket lätt. För att hitta det ömsesidiga av ett heltal beräknar du bara "1 (det numret)". För bråk är det ömsesidiga en annan bråkdel, det vill säga att talen är "inverterade" (invers).
- Till exempel motsatsen till 3/4 är 4/3.
- Varje tal när det multipliceras med dess ömsesidiga avkastning 1.
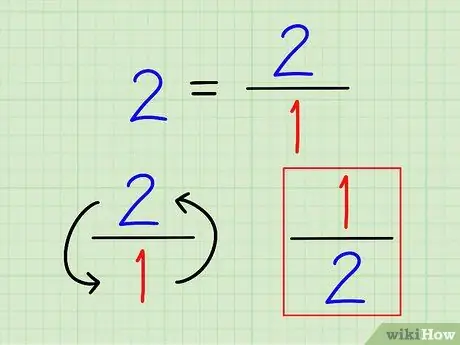
Steg 2. Skriv det ömsesidiga av hela talet som en bråkdel
Återigen är det ömsesidiga av ett tal alltid 1 (det numret). För heltal, skriv dem som bråk. Det är ingen idé att beräkna detta tal till en decimal.
Till exempel är det ömsesidiga av 2 1 = 1/2.
Metod 2 av 3: Hitta inversen av en blandad fraktion
Steg 1. Identifiera blandade nummer
Blandade bråk består av heltal och bråk, till exempel 24/5. Det finns två steg för att hitta det ömsesidiga av ett blandat antal enligt beskrivningen nedan.
Steg 2. Konvertera blandade tal till felaktiga fraktioner
Kom ihåg att 1 alltid kan skrivas som (nummer)/(samma tal) och fraktioner med samma nämnare (nedre tal) kan läggas ihop. Här är ett exempel med 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
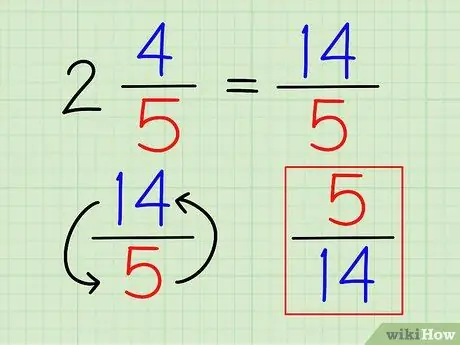
Steg 3. Vänd fraktionen
När numret väl skrivits helt som en bråkdel kan du hitta dess ömsesidiga precis som någon annan bråkdel, genom att vända fraktionen.
I exemplet ovan är det ömsesidiga av 14/5 är 5/14.
Metod 3 av 3: Hitta motsatsen till en decimal
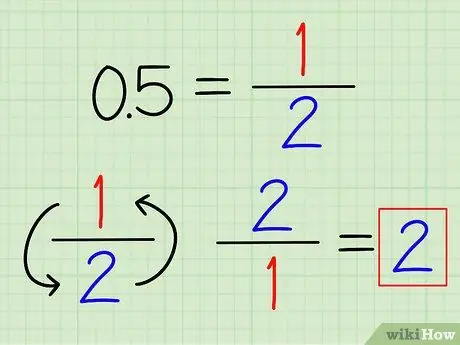
Steg 1. Om möjligt omvandla decimaler till bråk
Du kanske känner igen några ofta använda decimaltal, som enkelt kan konverteras till bråk. Till exempel 0,5 = 1/2 och 0,25 = 1/4. När decimalen har konverterats till en bråkdel vänder du bara bråket för att hitta dess ömsesidiga.
Till exempel är det ömsesidiga av 0,5 2/1 = 2.
Steg 2. Skriv ett uppdelningsproblem
Om du inte kan konvertera det till en bråkdel beräknar du det ömsesidiga antalet i form av ett divisionsproblem: 1 (decimal). Du kan använda en miniräknare för att lösa det eller gå vidare till nästa steg för att lösa det manuellt.
Till exempel kan du hitta det ömsesidiga av 0,4 genom att beräkna 1 0,4
Steg 3. Ändra divisionsproblemet för att använda heltal
Det första steget för att dela decimaler är att flytta decimalpunkten tills alla siffror är hela tal. Så länge du flyttar decimalpunkten för båda siffrorna med samma antal steg får du rätt svar.
Till exempel kan du använda 1 0, 4 och skriva om det som 10 4. I det här fallet flyttar du alla decimaler ett steg åt höger, på samma sätt som du multiplicerar varje tal med tio
Steg 4. Lös problemet med lång division
Använd metoden för lång delning för att beräkna det ömsesidiga. Om du räknar 10 4 får du svaret 2, 5 vilket är det ömsesidiga av 0, 4.
Tips
- Det negativa ömsesidiga för ett tal är detsamma som det vanliga ömsesidiga, genom att det multipliceras med det negativa. Till exempel det negativa ömsesidiga av 3/4 är -4/3.
- Det ömsesidiga eller ömsesidiga kallas ofta "multiplikationsinversen".
- Talet 1 är motsatsen till sig själv eftersom 1 1 = 1.
- Talet 0 har ingen ömsesidig eftersom 0 är odefinierad.
