- Författare Jason Gerald [email protected].
- Public 2024-01-15 08:24.
- Senast ändrad 2025-01-23 12:47.
Att dela en bråkdel med en bråkdel kan först verka förvirrande, men det är faktiskt väldigt enkelt. Allt du behöver göra är att vända, multiplicera och förenkla! Den här artikeln kommer att leda dig genom processen och visa dig hur lätt det är att dela en bråkdel med en bråkdel.
Steg
Del 1 av 2: Förstå hur man delar bråk med bråk
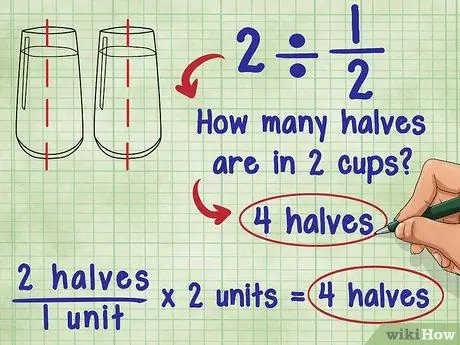
Steg 1. Tänk på vad delning med en bråkdel betyder
Handla om 2 ÷ 1/2 frågade Ada: "Hur många hälften är i två?" Svaret är 4 eftersom varje enhet (1) består av två "hälften", och det finns två totala enheter: 2 "halv"/1 enhet * 2 enheter = 4 "halv".
- Prova att föreställa dig samma ekvation med ett glas vatten: Hur många och ett halvt glas vatten finns i 2 glas vatten? Du kan hälla 2 och en halv kopp vatten i varje glas vatten. Det betyder att du i princip lägger till "halv" glas vatten och du har två glas: 2 "halv"/1 kopp * 2 koppar = 4 "halv".
- Det betyder att om fraktionen du delar är mellan 0 och 1, är svaret alltid större än det ursprungliga talet! Detta är sant när du delar ett heltal eller en bråkdel med en bråkdel.

Steg 2. Förstå att delning är motsatsen till att multiplicera
Sålunda kan delning med en fraktion lösas genom att multiplicera med den ömsesidiga fraktionen. Det ömsesidiga av en bråkdel (även kallad”multiplikationsinversen”) är fraktionen som är inverterad, så att täljaren och nämnaren byter plats. På ett ögonblick delar vi fraktioner med fraktioner genom att hitta den andra fraktionens ömsesidiga och multiplicera båda fraktionerna. Låt oss dock titta på några av motsatserna först:
- Det ömsesidiga av 3/4 är 4/3.
- Motsatsen till 7/5 är 5/7.
- Det ömsesidiga av 1/2 är 2/1 eller 2.
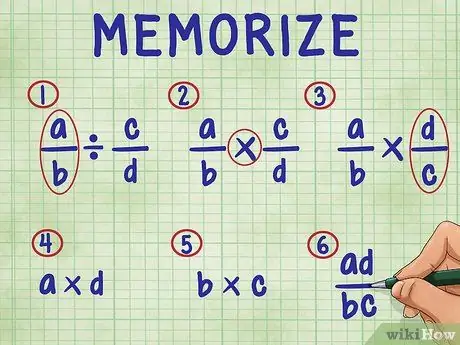
Steg 3. Kom ihåg följande steg för att dela en bråkdel med en bråkdel
I ordningen inkluderar stegen:
- Lämna bara den första fraktionen i ekvationen.
- Ändra divisionstecknet till multiplikationstecknet.
- Invertera den andra fraktionen (hitta dess ömsesidiga).
- Multiplicera täljaren (toppnummer) för båda fraktionerna. Multiplikationsresultatet är täljaren (överst) på ditt svar.
- Multiplicera nämnaren (nedre tal) för båda fraktionerna. Produkten av produkten är nämnaren för ditt svar.
- Förenkla dina fraktioner genom att förenkla dem till deras enklaste termer.
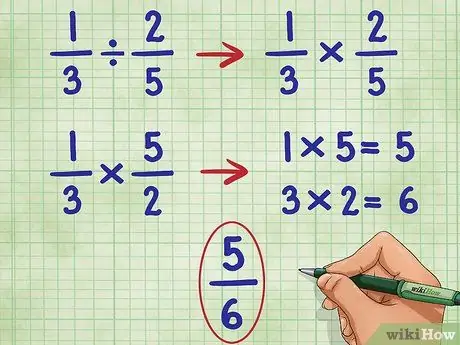
Steg 4. Utför dessa steg för 1/3 2/5 exemplet
Vi börjar med att utelämna den första fraktionen och konvertera divisionstecknet till multiplikationstecknet:
- 1/3 ÷ 2/5 = Blir:
- 1/3 * _ =
- Nu vänder vi den andra fraktionen (2/5) för att hitta dess ömsesidiga, vilket är 5/2:
- 1/3 * 5/2 =
- Nu multiplicera täljaren (toppnummer) för båda fraktionerna, 1*5 = 5.
- 1/3 * 5/2 = 5/
- Nu multiplicera nämnaren (nedre tal) för båda fraktionerna, 3*2 = 6.
- Nu har vi: 1/3 * 5/2 = 5/6
- Denna fraktion kan inte förenklas ytterligare, så vi har vårt svar.

Steg 5. Försök att komma ihåg följande rim för att hjälpa dig komma ihåg:
"Att dela upp fraktioner är enkelt, vänd den andra fraktionen och multiplicera sedan. Glöm inte att förenkla innan det är dags att äta."
En annan hjälpsam påminnelsehjälp berättar vad du ska göra med varje del av ekvationen:”Låt mig (första bråk), Ändra mig (delningstecken), Vänd mig (andra bråk).”
Del 2 av 2: Dela bråk med bråk i problem
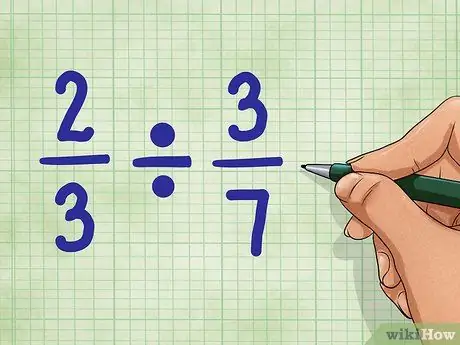
Steg 1. Börja med exempelfrågor
Låt oss använda 2/3 ÷ 3/7. Denna fråga ber om antalet delar lika med 3/7, som finns i värdet 2/3. Oroa dig inte. Det är inte så svårt som det låter!
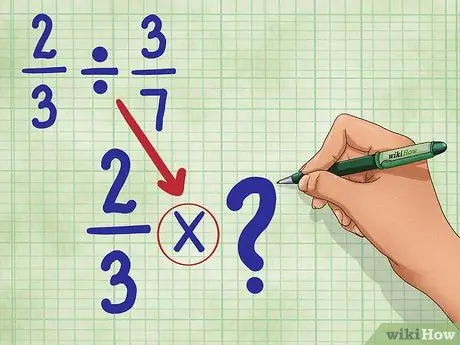
Steg 2. Konvertera divisionstecknet till multiplikationstecknet
Din nya ekvation kommer att vara: 2/3 * _ (Vi fyller det här tomt om en stund.)
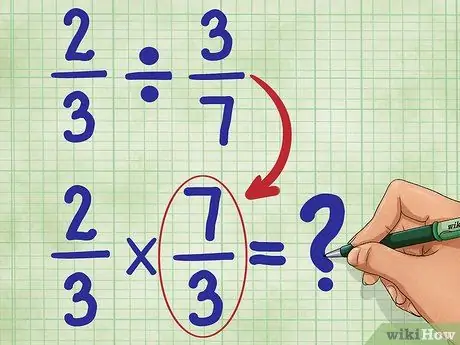
Steg 3. Hitta nu det ömsesidiga för den andra fraktionen
Detta innebär att vi vänder 3/7 så att täljaren (3) nu är längst ner och nämnaren (7) nu är överst. Det ömsesidiga av 3/7 är 7/3. Skriv nu din nya ekvation:
2/3 * 7/3 = _

Steg 4. Multiplicera dina fraktioner
Multiplicera först täljarna för båda fraktionerna: 2 * 7 = 14. 14 är täljaren (toppnummer) för ditt svar. Multiplicera sedan nämnare för båda fraktionerna: 3 * 3 = 9. 9 är nämnaren (bottennummer) för ditt svar. Nu vet du det 2/3 * 7/3 = 14/9.
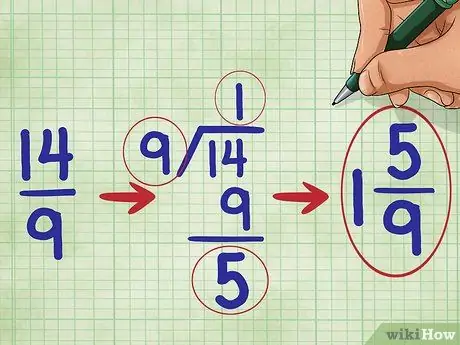
Steg 5. Förenkla din bråkdel
I detta problem, eftersom täljaren för fraktionen är större än nämnaren, vet vi att vår bråk är större än 1. Vi måste konvertera den till ett blandat tal. (Ett blandat tal är ett heltal och en bråkdel kombinerat, till exempel 1 2/3.))
-
Dela först täljaren
Steg 14. med 9.
Talet 14 dividerat med 9 är lika med ett med resten av 5, så du bör skriva ner din förenklade bråkdel som: 1 5/9 ("En fem-nionde").
- Sluta, du har hittat svaret! Du kan ange att du inte kan förenkla bråket längre eftersom nämnaren inte är delbar med täljaren (9 är inte delbar med 5) och täljaren är ett primtal, eller ett heltal som bara är delbart med en och själva talet.
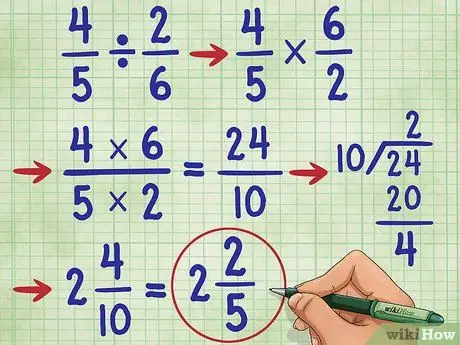
Steg 6. Prova ett annat exempel
Låt oss testa frågan 4/5 ÷ 2/6 =. Ändra först divisionstecknet till multiplikationstecknet (4/5 * _ =), hitta sedan det ömsesidiga av 2/6, vilket är 6/2. Nu har du ekvationen: 4/5 * 6/2 =_. Nu multiplicera täljaren, 4 * 6 = 24och nämnaren 5* 2 = 10. Nu har du 4/5 * 6/2 = 24/10.
Förenkla nu fraktionen. Eftersom täljaren är större än nämnaren måste vi omvandla denna bråkdel till ett blandat tal.
- Dela först täljaren med nämnaren, (24/10 = 2 återstående 4).
- Skriv svaret som 2 4/10. Vi kan fortfarande förenkla denna fraktion igen!
- Observera att 4 och 10 är jämna tal. Så, det första steget för att förenkla det är att dela varje tal med 2. Vi får 2/5.
- Eftersom nämnaren (5) inte är delbar med täljaren (2) och 5 är ett primtal, vet vi att denna bråkdel inte kan förenklas ytterligare. Så vårt svar är: 2 2/5.

Steg 7. Få ytterligare hjälp med att förenkla fraktioner
Du har förmodligen spenderat mycket tid på att lära dig hur du förenklar bråk innan du försöker dela dem med varandra. Men om du behöver en uppdatering eller annan hjälp finns det några bra artiklar på nätet som kan vara till stor hjälp för dig.
Relaterade wikiHow -artiklar
- Konvertera vanliga bråk till decimaler
- Beräkning av en cirkels yta
- Dela polynom med syntetisk division
- Dela blandade fraktioner






