Så länge du vet måttet för de andra två vinklarna är det enkelt att hitta den tredje vinkeln i en triangel. Du behöver bara subtrahera summan av de två vinklarna med 180 grader. Men det finns också andra sätt som du kan använda för att hitta den tredje vinkeln i en triangel om problemets form är lite annorlunda än vanligt. Om du vill veta hur du hittar den tredje vinkeln i en triangel, följ guiden nedan.
Steg
Metod 1 av 3: Använda måtten för de andra två vinklarna
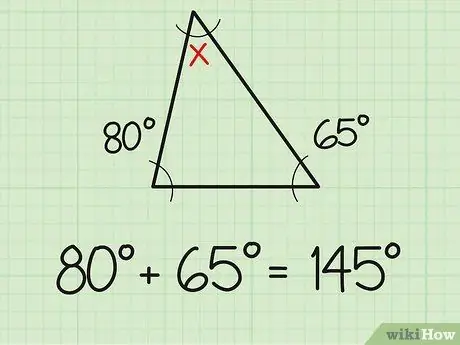
Steg 1. Lägg ihop de två kända vinklarna
Ett faktum du bör veta är att summan av de tre vinklarna i en triangel alltid är 180 grader. Så om du redan känner till måttet på de två vinklarna i en triangel är det lika enkelt att hitta den tredje vinkeln som att göra enkla additions- och subtraktionsproblem. Lägg först ihop de två vinkelmåtten du redan känner till. Till exempel mäter två kända vinklar 80 och 65 grader. Lägg ihop de två (80+65) så får du 145 grader.
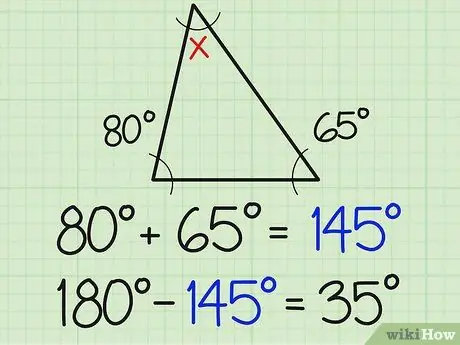
Steg 2. Dela det numret med 180
Summan av de tre vinklarna i en triangel är alltid 180 grader. Därför måste den tredje vinkeln vara 180 när den läggs till summan av de två kända måtten på vinkeln. I exemplet ovan betyder detta 180-154 = 35.
Steg 3. Skriv ditt svar
Nu har du svaret på den tredje vinkeln (i exemplet 35 grader). Om du fortfarande är i tvivel, se själv. Lägg ihop de tre vinklarna så får du ett resultat på 180. Om du inte gör det är din beräkning fel. För detta exempel, 80+65+35 = 180. Om det är korrekt betyder det att du har löst problemet.
Metod 2 av 3: Använda variabler
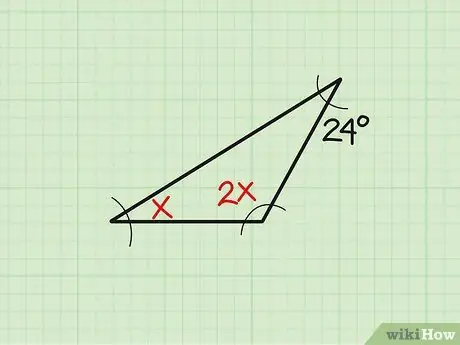
Steg 1. Skriv ner problemet
Ibland visas storleken på den befintliga vinkeln i en variabel form. Låt oss ta detta exempel: "Hitta vinkeln" x "i en triangel om de tre vinklarna mäter" x "," 2x "respektive 24." Skriv först ner problemet.
Steg 2. Lägg ihop alla vinkelmått
Principen du måste komma ihåg är densamma. Så lägg först ihop de tre vinklarna i problemet, nämligen "x+2x+24 = 3x+24".
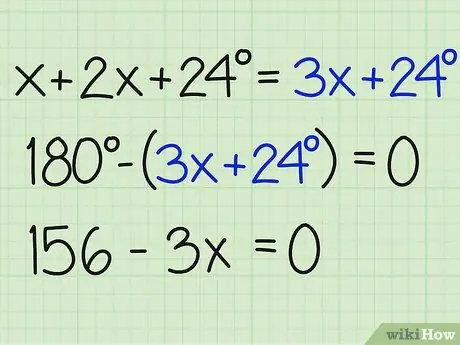
Steg 3. Dela summan av vinklarna med 180
Skill det numret med 180 grader för att hitta x och ta reda på svaret på problemet. Se till att du avslutar ekvationen lika med noll. Så här är det skrivet:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
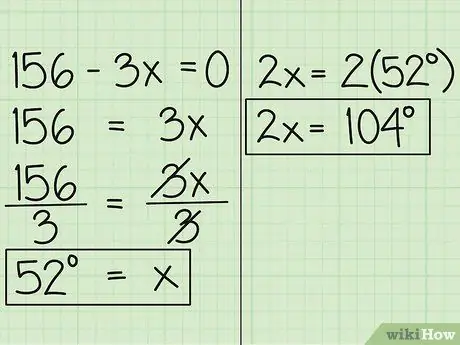
Steg 4. Hitta värdet på x
Flytta nu variabeln till den andra sidan av ekvationen, så får du 156 = 3x. Dela sedan ekvationen med 3, så får du x = 52. Det betyder att måttet på vinkeln uttryckt i x är 52 grader. Den andra vinkeln, uttryckt i 2x är 52 grader gånger 2, vilket är 104 grader.
Steg 5. Kontrollera dina resultat
Om du vill se till att ditt svar är korrekt, lägg bara till de tre vinkelmått som du redan har hittat svaret på. Om resultatet är 180 betyder det att ditt svar är korrekt. För detta exempel, 52+104+24 = 180.
Metod 3 av 3: Använda andra metoder
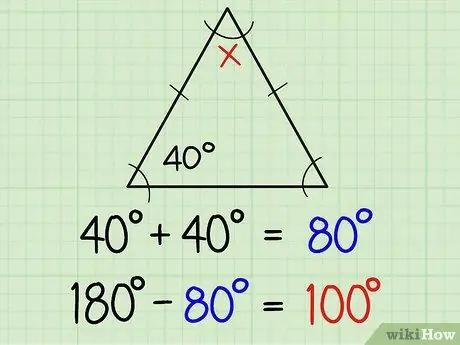
Steg 1. Hitta vinklarna på en likbent triangel
En likbent triangel har två lika sidor och två lika vinklar. Två lika sidor är vanligtvis markerade med en liten linje mitt på sidlinjen, vilket innebär att de två motsatta vinklarna på linjen är samma mått. Om du redan vet storleken på den ena vinkeln, känner du automatiskt till den andra vinkeln. Här är ytterligare förklaring:
Om en av de lika vinklarna är 40 grader, är den andra 40 grader. På så sätt kan du hitta alla tre vinklarna med skillnaden mellan summan av 40+40 (dvs. 80) och 180, eller med andra ord 180-80 = 100
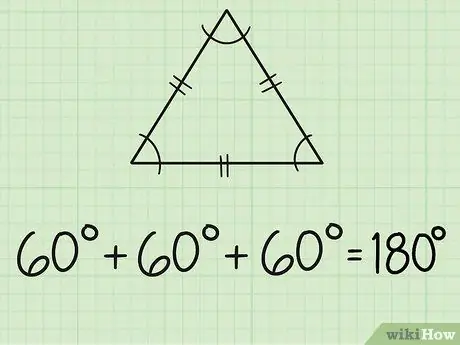
Steg 2. Hitta vinklarna på en liksidig triangel
En liksidig triangel har tre lika sidor och tre lika vinklar. Varje sida är vanligtvis markerad med två korta linjer i mitten. Eftersom alla tre vinklarna är lika betyder det att alla vinklar mäter 60 grader, eftersom 180/3 = 60.
Steg 3. Hitta den tredje vinkeln i en rätt triangel
Antag att du får en rätt triangel, med en av spetsiga vinklar som mäter 30 grader. Eftersom triangeln är en rät vinkel betyder det att en av vinklarna, nämligen rätt vinkel, måste mäta 90 grader. Använd sedan triangelprincipen, skillnaden mellan summan av de två vinklarna (90+30 = 120) med 180, då får du 180-120 = 60 grader.
