Vet du inte hur man ritar linjära ekvationer utan att använda en miniräknare? Lyckligtvis är det ganska enkelt att rita linjära ekvationer om du vet hur. Allt du behöver göra är att förstå några saker om din ekvation och du kommer att kunna göra det. Låt oss börja.
Steg
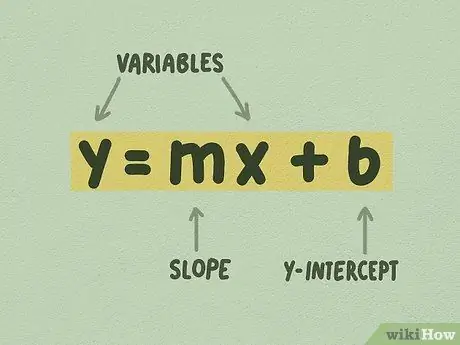
Steg 1. Se till att den linjära ekvationen har formen y = mx + b
Denna form kallas y-skärningsformen och är förmodligen den enklaste formen att använda för att rita linjära ekvationer. Värdet i ekvationen behöver inte vara ett heltal. Ofta ser du en ekvation som ser ut så här: y = 1/4x + 5, där 1/4 är m och 5 är b.
- m kallas "lutningen", eller ibland "lutningen". Lutningen definieras som ökningen över sidan, eller förändringen i y dividerat med förändringen i x.
- b definieras som "y-skärning". Y-skärningen är den punkt där linjen skär Y-axeln.
- x och y är variabler. Du kan lösa för ett specifikt x -värde, till exempel om du har en punkt y och känner till värdena för m och b. X har dock aldrig bara ett värde: dess värde ändras när raden går upp eller ner.
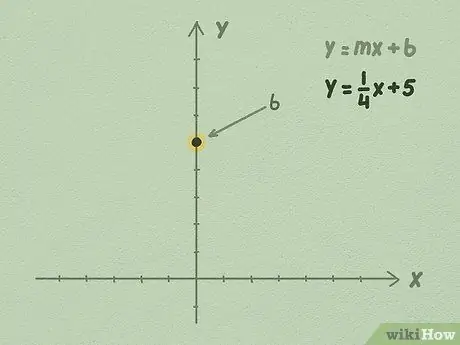
Steg 2. Rita talet b på Y -axeln
Ditt b -värde kommer alltid att vara ett rationellt tal. Oavsett vilket nummer b är, hitta dess värde på Y -axeln och placera numret vid en punkt på den vertikala axeln.
Till exempel, låt oss använda ekvationen y = 1/4x + 5. Eftersom det sista talet är b, vet vi att b är lika med 5. Flytta upp 5 punkter på Y -axeln och markera punkterna. Det är här din raka linje skär Y -axeln
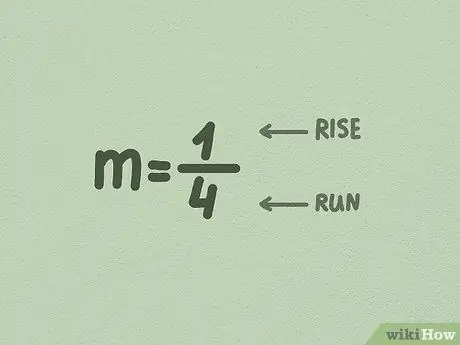
Steg 3. Konvertera m till en bråkdel
Ofta är talet framför x redan en bråkdel, så du behöver inte ändra det. Men om inte, bara ändra det genom att placera värdet på m under talet 1.
- Det första numret (täljaren) är ökningen i stigande dividerat med sidan. Detta nummer anger hur långt linjen går upp, eller vertikalt.
- Det andra talet (nämnaren) är sidan i stigande dividerat med sidan. Detta nummer anger hur långt linjen rör sig i sidled eller horisontellt.
- Till exempel:
- Lutningen 4/1 flyttar 4 poäng upp för varje 1 poäng åt sidan.
- Lutningen på -2/1 flyttar 2 poäng nedåt för varje 1 poäng åt sidan.
- En lutning på 1/5 rör sig 1 poäng upp för varje 5 poäng åt sidan.
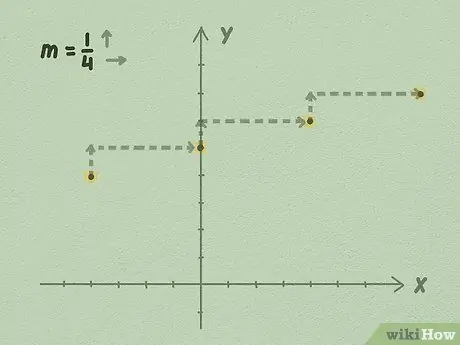
Steg 4. Börja förlänga linjen från b med lutningen, eller uppåt dividerat med sidan
Börja med ditt b -värde: vi vet att ekvationen går förbi denna punkt. Förläng linjen genom att ta din lutning och använda dess värde för att få poängen i ekvationen.
- Till exempel, med hjälp av illustrationen ovan, kan du se att för varje 1 poäng uppåt flyttas linjen 4 punkter till höger. Detta händer eftersom linjens lutning är 1/4. Du förlänger linjen på obestämd tid till båda sidor, fortsätter att använda upp dividerat med sidan för att rita linjen.
- Lutningen är positiv när du flyttar upp, medan lutningen är negativ när du flyttar ner. En lutning på -1/4, till exempel, kommer att gå ner 1 poäng för varje 4 poäng i sidled.
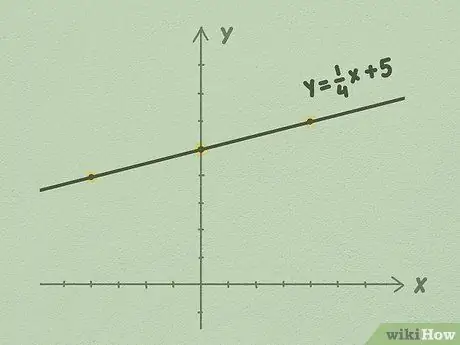
Steg 5. Fortsätt att förlänga linjen, använda en linjal och se till att använda lutningen, m, som en guide
Förläng linjen på obestämd tid och du är klar med att rita din linjära ekvation. Ganska lätt, eller hur?
