3 sätt att beräkna hastighet

2024 Författare: Jason Gerald | [email protected]. Senast ändrad: 2024-01-16 19:59

Hastighet är en beräkning av hur snabbt något rör sig på en gång. Om du någonsin har tittat på hastighetsmätaren för en bil i rörelse ser du hastighetsräkningen - ju längre nålen färdas, desto högre blir fordonets hastighet. Det finns flera sätt att beräkna hastighet, beroende på vilken typ av information du har. I allmänhet formeln hastighet = distans/tid (eller k = j/w) är det enklaste sättet att beräkna hastighet.

Steg

Metod 1 av 3: Använda standardhastighetsberäkningsformler

Steg 1. Hitta avståndet ett objekt har rest

Den grundläggande formeln som de flesta använder för att hitta hastigheten på något är mycket lätt att använda. Först och främst måste du veta "hur mycket avstånd har det uppmätta objektet rest". Med andra ord, vad är avståndet mellan objektets startpunkt och slutpunkt?

Denna formel är lättare att förstå genom ett exempel. Låt oss säga att vi reser med bil till en lekplats för "161 kilometer". I några steg kan vi använda denna information för att slutföra beräkningen av formeln

Steg 2. Hitta den tid det tar föremålet att resa den sträckan

Nästa information du behöver är hur lång tid det tar för objektet att nå ett visst avstånd. Med andra ord, hur lång tid tar det för objektet att flytta från startpunkten till slutpunkten?

I det här exemplet, låt oss säga att objektet tar ca. två timmar för att komma till destinationen.

Steg 3. Dela avståndet med den tid det tar att hitta objektets hastighet

Du behöver bara dessa två uppgifter för att veta objektets hastighet. Avståndet till tiden är lika med objektets hastighet.

I det här exemplet, 161 kilometer/2 timmar = 80,5 kilometer/timme.

Steg 4. Glöm inte den använda enheten

Det är mycket viktigt att använda rätt enheter i ditt svar (t.ex. kilometer i timmen, etc.) Utan dessa enheter är det mycket svårt för människor att förstå innebörden av ditt svar. Du kan också tappa poäng om du använder fel enhet när du utför uppgifter från skolan.

Enheten för hastighet är avståndsenhet till tidsenhet. Till exempel, eftersom vi mäter avstånd i kilometer och tid i timmar, är de enheter som används kilometer/timme (eller kilometer i timmen).

Metod 2 av 3: Lösa svårare beräkningar

Steg 1. Hitta flera olika variabler för att lösa problemet med avstånd och tid

När du väl har förstått grundformeln för hastighet kan du använda den för att utföra andra beräkningar än hastighet. Till exempel, om du till en början bara känner till objektets hastighet och en annan variabel kan du ordna om formeln ovan för att hitta okänd information.

Låt oss till exempel säga att vi vet att ett tåg färdas med 20 kilometer i timmen i fyra timmar, men vi vet inte hur långt det har rest. För att ta reda på det kan vi ordna om formeln på följande sätt:

hastighet = distans/tid

hastighet × tid = (distans/tid) × tid

hastighet × tid = avstånd

20 km/timme × 4 timmar = avstånd = 80 kilometer

Steg 2. Konvertera de enheter du använder efter behov

Ibland kan du beräkna hastigheten med en viss enhet, men måste konvertera den till en annan enhet. I det här fallet måste du använda en konverteringsfaktor för att få svaret enligt rätt enheter. För att göra detta, skriv helt enkelt förhållandet mellan enheterna i bråkform och multiplicera. Vid multiplicering, vänd fraktionen efter behov för att ta bort oönskade enheter. Denna metod är mycket enklare än den låter!

Låt oss till exempel säga att i exempelproblemet ovan behöver vi svaret i miles istället för i kilometer. En mil är ungefär 1,6 kilometer. Så vi kan göra konverteringen enligt följande:

80 kilometer × 1,6 kilometer = 50 mil
Kom ihåg att eftersom kilometer visas längst ner i fraktionen tar det bort kilometer från föregående svar, så det slutliga resultatet använder miles.
Denna webbplats erbjuder konverteringsfunktioner för de flesta vanliga enheterna.

Steg 3. Ersätt variabeln "avstånd" med avståndsformeln efter behov

Objekt rör sig inte alltid i en rak, jämn bana. Om detta är sant kanske du inte bara kan ange ett numeriskt värde som en avståndsenhet i standardhastighetsformeln. Du kan dock behöva ersätta bokstaven j i formeln k = j/w med en formel som liknar den sträcka som objektet reste.

Låt oss till exempel säga att ett flygplan roterar genom luften ett avstånd på 20 miles 5 gånger. Planet slutförde omgången på en halvtimme. I det här exemplet behöver vi fortfarande hitta den totala sträckan som planet reste innan vi kan bestämma dess hastighet. Vi kan använda formeln för att beräkna avståndet runt en cirkel (avståndet runt den) istället för j i denna formel. Denna formel är omkrets = 2πr där r = cirkelradie. Så här löser du det:

k = (2 × × r)/w

k = (2 × × 10)/0,5

k = 62,83/0,5 = 125,66 miles/timme

Steg 4. Förstå att k = j/w ger medelhastigheten

Den enkla och enkla formeln vi använder för att hitta hastighet har en nackdel. Det resulterande värdet är tekniskt sett medelhastigheten. Det betyder att formeln antar att objektet du mäter använder samma hastighet som det rör sig. Som vi kommer att se nedan blir det mycket svårare att hitta ett objekts hastighet i ett enda ögonblick.

För att illustrera denna skillnad, tänk dig förra gången du reste med bil. Det är osannolikt att du reser i samma hastighet som du reser. Men vanligtvis börjar du din resa med låg hastighet och gradvis ökar din hastighet under vägen, stannar på grund av rött ljus, trafikstockningar etc. Om du använder standardhastighetsformeln för att hitta hastighet under resan kan ändringar av den hastigheten inte upptäckas. Du får dock ett svar som visar medelhastigheten för alla hastighetsskillnader du reser

Metod 3 av 3: Beräkning av omedelbar hastighet

Notera:

Detta avsnitt använder tekniker som är mindre bekanta för personer som aldrig har studerat kalkyl. Läs våra artiklar om kalkyl för hjälp.

Steg 1. Förstå att hastigheten definieras som accelerationshastigheten

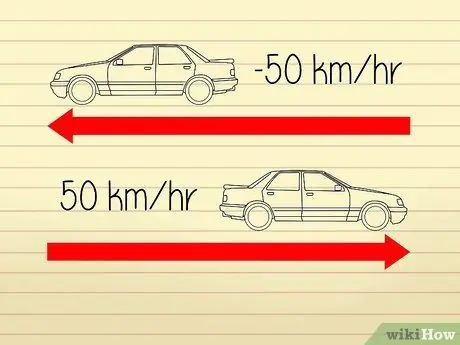
Hög hastighetsberäkningar är ganska förvirrande eftersom matematiker och forskare använder olika definitioner för att beskriva "hastighet" och "acceleration". Acceleration har två komponenter: en "hastighet" och en "riktning". Hastigheten är lika med objektets hastighet. En riktningsförändring kommer att orsaka en förändring av accelerationen, men inte en förändring av hastigheten.

Låt oss till exempel säga att två bilar rör sig i motsatta riktningar. Hastighetsmätarna på båda bilarna visar en siffra på 50 km/h så att de båda kör i samma hastighet. Men eftersom bilarna rör sig bort från varandra kan vi säga att en av bilarna har en”acceleration” på -50 km/h medan den andra har en”acceleration” på 50 km/h.
Precis som momentana hastighetsberäkningar kan du också utföra momentana accelerationsberäkningar.

Steg 2. Använd absoluta värden för att mäta negativ acceleration

Ett objekt kan ha en negativ accelerationshastighet (om det rör sig i en negativ riktning i förhållande till ett annat objekt). Det finns dock ingen negativ hastighet. Så i detta fall indikerar hastighetens absoluta värde objektets hastighet.

Av detta skäl, i exemplet ovan, har båda bilarna en hastighet av 50 km/h.

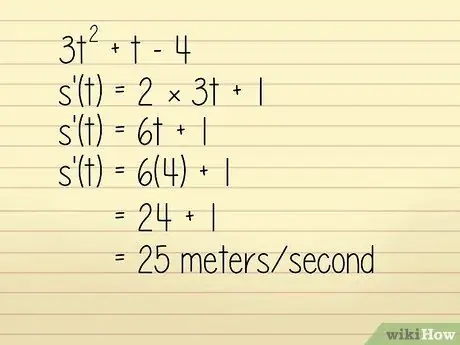
Steg 3. Ta derivatet av funktionens position

Om du har en funktion k (w) som visar positionen för ett objekt utan att behöva beräkna tiden, kommer derivatet av k (w) att visa accelerationen utan behov av tidtagning. Anslut bara tidsvärdet till denna formel så att variabeln w (eller vilket tidsvärde som helst används) accelereras enligt den tiden. Härifrån kan du enkelt hitta objektets hastighet.

Låt oss till exempel säga att positionen för ett objekt i en meter beskrivs i ekvationen 3q² + w - 4 där w = tid i sekunder. Vi vill veta objektets hastighet vid w = 4 sekunder. I det här fallet kan du lösa det genom att:

3w² +w - 4

k '(w) = 2 × 3w + 1

k '(w) = 6w + 1
Nu anger vi w = 4:

k '(w) = 6 (4) + 1 = 24 + 1 = 25 meter/sekund. Tekniskt sett är detta en beräkning av acceleration, men eftersom den är positiv och riktningen inte nämns i frågan kan vi använda den för att hitta hastighet.

Steg 4. Ta den integrerade accelerationsfunktionen

Acceleration är ett sätt att mäta förändringen i ett föremåls acceleration över tid. Detta ämne är för komplext för att förklaras fullständigt i den här artikeln. Det är dock användbart att notera att när du har en funktion a (w) som representerar acceleration med avseende på tid, kommer integralen av a (w) att returnera resultatet av acceleration baserat på den tiden. Kom ihåg att det är mycket användbart att känna till den ursprungliga accelerationen för ett objekt så att du kan definiera konstanten för det resultatet från en oändlig integral.

Låt oss till exempel säga att ett objekt har en konstant acceleration (i m/s² som ett resultat av a (w) = -30. Säg också att objektet har en initial acceleration på 10 m/s. Vi måste hitta hastigheten vid w = 12 sekunder. I det här fallet kan vi lösa det genom att:

a (w) = -30

p (w) = a (w) dw = -30dw = -30w + C
För att hitta C löser vi p (w) för w = 0. Kom ihåg att objektets initiala acceleration är 10 m/s.

p (0) = 10 = -30 (0) + C

10 = C, så p (w) = -30w + 10
Nu kan vi ange w = 12 sekunder.

p (12) = -30 (12) + 10 = -360 + 10 = -350. Eftersom hastigheten är ett absolut accelerationsvärde är objektets hastighet 350 meter/sekund.

Tips

Övning gör bra! Försök skapa din egen fråga genom att ersätta siffrorna i exemplet ovan.
Om du letar efter ett snabbt sätt att öva kalkyl för bättre beräkningshastighet, använd onlinederivatkalkylatorn här och online -integralkalkylatorn här.