- Författare Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:24.
- Senast ändrad 2025-01-23 12:47.
Den normala kraften är storleken på den kraft som krävs för att negera de andra krafterna i vilket scenario som helst. Det bästa sättet att hitta det beror på objektets skick och de variabler du har. Fortsätt läsa för att lära dig mer.
Steg
Metod 1 av 5: Normal stil i vila
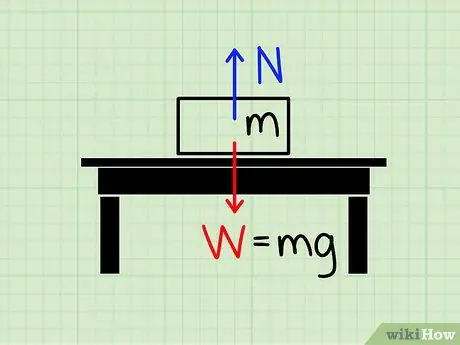
Steg 1. Förstå betydelsen av normal kraft
Den normala kraften avser storleken på den kraft som används för att negera gravitationskraften.
Föreställ dig ett block i vila på ett bord. Tyngdkraften drar blocket mot jorden, men det är klart att det verkar en kraft som hindrar blocket från att krossa bordet och falla till marken. Kraften som verkar för att stoppa detta block trots tyngdkraften kallas normal stil.
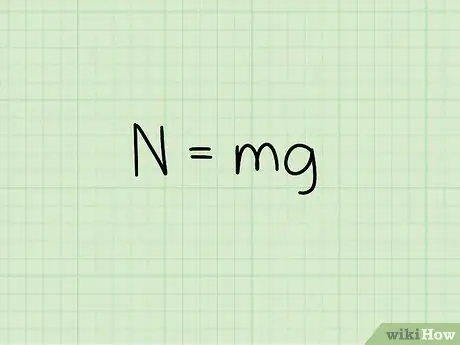
Steg 2. Känn ekvationen för den normala kraften på ett föremål i vila
När du beräknar ett objekts normalkraft när det vilar på en plan yta, använd formeln: N = m * g
- I denna ekvation, N symboliserar normal stil, m representerar objektets massa och g representerar accelerationen på grund av gravitationen.
- För ett föremål som vilar på en plan yta, utan att en yttre kraft verkar, är den normala kraften lika med objektets vikt. För att hålla ett föremål i vila måste den normala kraften vara lika med gravitationskraften som verkar på föremålet. Gravitationskraften som verkar på ett objekt är objektets vikt, eller objektets massa gånger accelerationen på grund av gravitationen.
- Exempel: Hitta den normala kraften för ett block med en massa på 4,2 kg.
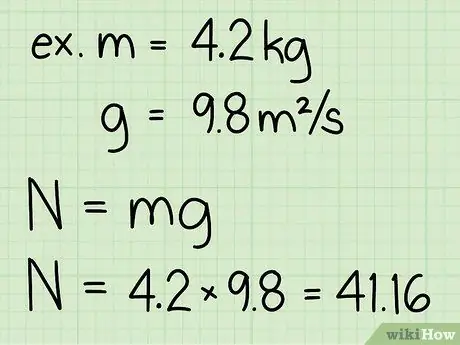
Steg 3. Multiplicera objektets massa och accelerationen på grund av gravitationen
Denna multiplikation kommer att producera objektets vikt, vilket naturligtvis är lika med objektets normalkraft i vila.
- Observera att accelerationen på grund av gravitationen på jordytan alltid är konstant: g = 9,8 m/s2
- Exempel: vikt = m * g = 4, 2 * 9, 8 = 41, 16

Steg 4. Skriv ner dina svar
Det föregående steget kommer att lösa problemet och ge dig ditt svar.
Exempel: Normalkraften är 41, 16 N
Metod 2 av 5: Normal kraft på ett lutande plan
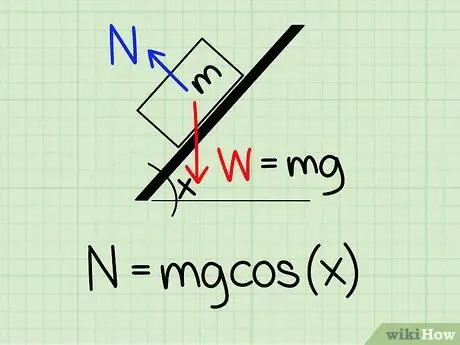
Steg 1. Använd rätt ekvation
För att beräkna normalkraften på ett föremål lutat med en viss vinkel måste du använda formeln: N = m * g * cos (x)
- För denna ekvation, N symboliserar normal stil, m representerar objektets massa g representerar accelerationen på grund av gravitationen och x representerar den sneda vinkeln.
- Exempel: Hitta den normala kraften för ett block med en massa på 4,2 kg, som vilar på ett lutande plan med en lutning på 45 grader.

Steg 2. Hitta cosinus för vinkeln
Cosinus för vinkeln är lika med sinus för den komplementära vinkeln, eller den intilliggande sidan dividerad med hypotenusen i triangeln som bildas av lutningen.
- Detta värde bestäms ofta med en miniräknare eftersom cosinus för valfri vinkel alltid är konstant, men du kan också beräkna det manuellt.
- Exempel: cos (45) = 0,71
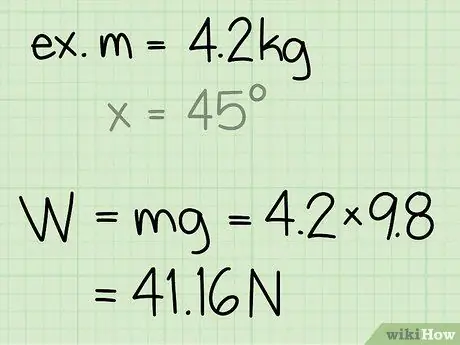
Steg 3. Hitta objektets vikt
Objektets vikt är lika med objektets massa gånger accelerationen på grund av gravitationen.
- Observera att accelerationen på grund av gravitationen på jordytan alltid är konstant: g = 9,8 m/s2
- Exempel: vikt = m * g = 4, 2 * 9, 8 = 41, 16
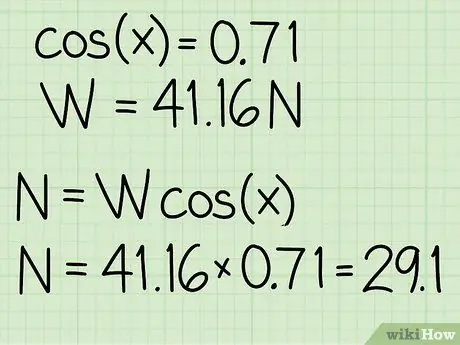
Steg 4. Multiplicera de två värdena
För att hitta den normala kraften måste du multiplicera objektets vikt med cosinus för lutningsvinkeln.
Exempel: N = m * g * cos (x) = 41, 16 * 0, 71 = 29, 1
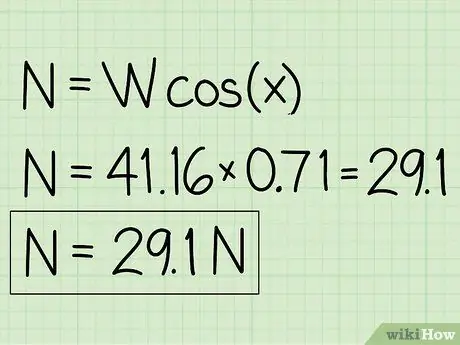
Steg 5. Skriv ner dina svar
Det föregående steget kommer att lösa problemet och ge ditt svar.
- Observera att när ett föremål vilar på en lutning kommer den normala kraften att vara mindre än objektets vikt.
- Exempel: Normalkraften är 29,1 N.
Metod 3 av 5: Normal stil med yttre ned -stil
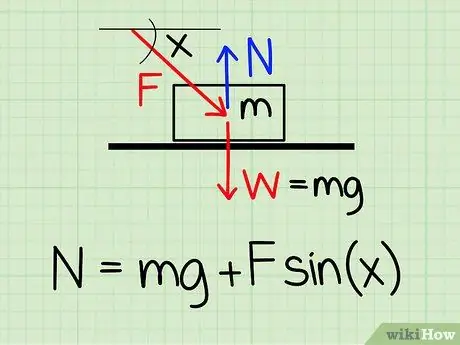
Steg 1. Använd rätt ekvation
För att beräkna normalkraften på ett objekt i vila om det finns en yttre nedåtriktad kraft på objektet, använd ekvationen: N = m * g + F * sin (x) '
- N symboliserar normal stil, m representerar objektets massa g representerar accelerationen på grund av tyngdkraften, F symboliserar yttre stil, och x representerar vinkeln mellan objektet och riktningen för den yttre kraften.
- Exempel: Hitta den normala kraften för ett föremål med en massa på 4,2 kg om objektet trycks av en person i en vinkel på 30 grader och en kraft på 20,9 N.
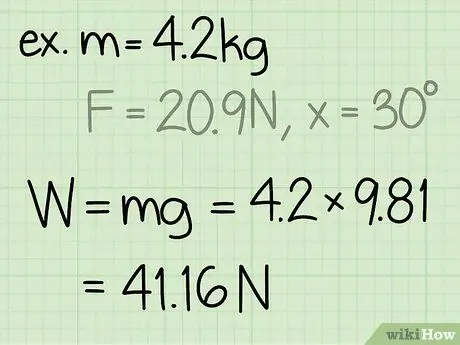
Steg 2. Hitta objektets vikt
Objektets vikt är lika med objektets massa gånger accelerationen på grund av gravitationen.
- Observera att accelerationen på grund av gravitationen på jordytan alltid är konstant: g = 9,8 m/s2
- Exempel: vikt = m * g = 4, 2 * 9, 8 = 41, 16
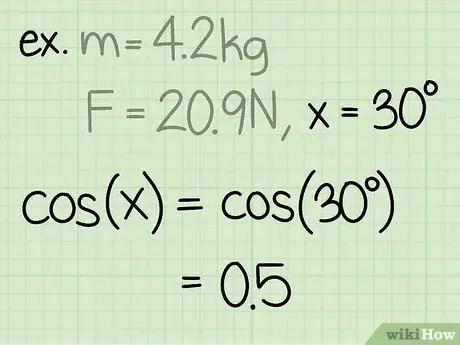
Steg 3. Hitta sinus för vinkeln
Sinusen för en vinkel beräknas genom att dividera sidan av triangeln motsatt vinkeln, med vinkelns hypotenusa.
Exempel: sin (30) = 0,5

Steg 4. Multiplicera sinus med den yttre kraften
Extern kraft, i detta exempel, avser den nedåtriktade kraften som träffar objektet.
Exempel: 0, 5 * 20, 9 = 10, 45
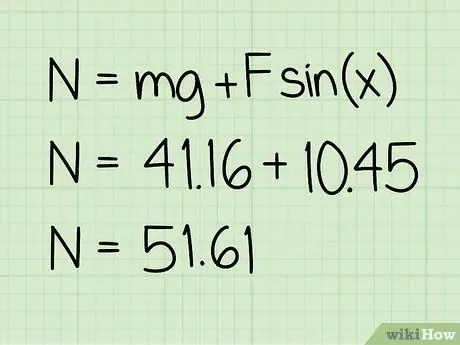
Steg 5. Lägg till detta värde i vikten
Denna summa ger storleken på den normala kraft som verkar.
Exempel: 10, 45 + 41, 16 = 51, 61
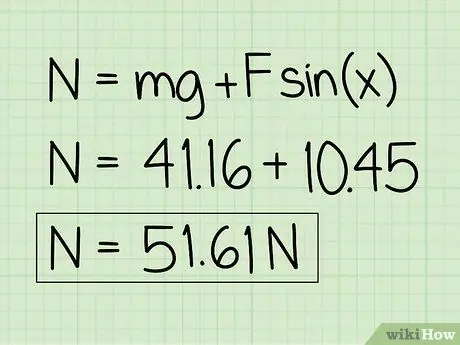
Steg 6. Skriv ner dina svar
Observera att för ett föremål i vila som påverkas av en yttre nedåtgående kraft kommer den normala kraften att vara större än föremålets vikt.
Exempel: Normalkraften är 51,61 N
Metod 4 av 5: Normal stil med yttre stil upp
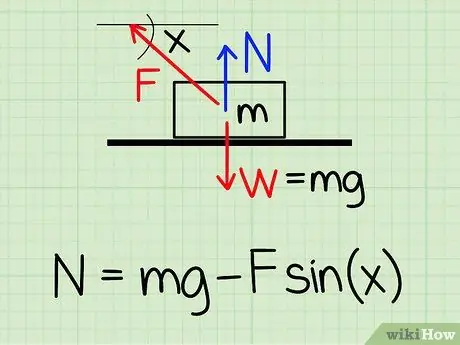
Steg 1. Använd rätt ekvation
För att beräkna normalkraften på ett föremål i vila om det finns en yttre uppåtriktad kraft på objektet, använd ekvationen: N = m * g - F * sin (x) '
- N symboliserar normal stil, m representerar objektets massa g representerar accelerationen på grund av tyngdkraften, F symboliserar yttre stil, och x representerar vinkeln mellan objektet och riktningen för den yttre kraften.
- Exempel: Hitta den normala kraften för ett block med en massa på 4,2 kg, om någon drar upp blocket i en vinkel på 50 grader och en kraft på 20,9 N.

Steg 2. Hitta objektets vikt
Objektets vikt är lika med objektets massa gånger accelerationen på grund av gravitationen.
- Observera att accelerationen på grund av gravitationen på jordytan alltid är konstant: g = 9,8 m/s2
- Exempel: vikt = m * g = 4, 2 * 9, 8 = 41, 16
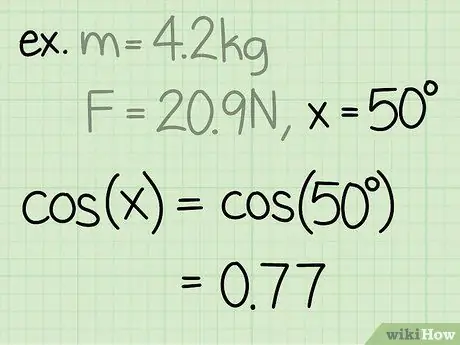
Steg 3. Hitta sinus för vinkeln
Sinusen för en vinkel beräknas genom att dividera sidan av triangeln motsatt vinkeln, med vinkelns hypotenusa.
Exempel: sin (50) = 0, 77

Steg 4. Multiplicera sinus med den yttre kraften
Extern kraft avser den uppåtriktade kraft som träffar objektet, i detta fall.
Exempel: 0,77 * 20, 9 = 16, 01
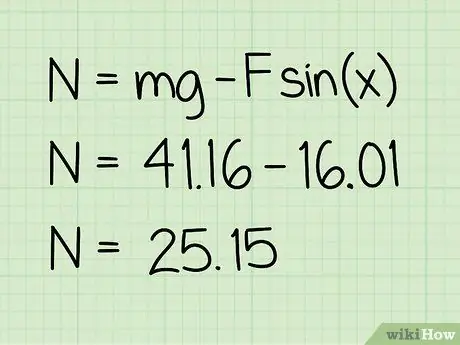
Steg 5. subtrahera detta värde från vikten
Subtraktionen du gör ger dig storleken på den normala kraft som verkar på den.
Exempel: 41, 16 - 16, 01 = 25, 15
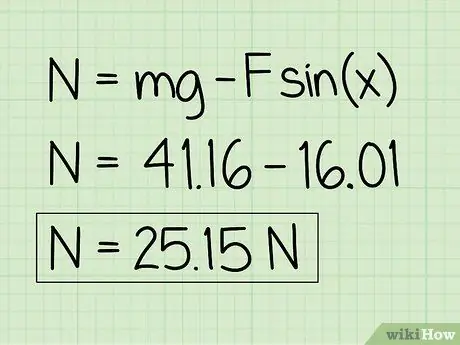
Steg 6. Skriv ner dina svar
Observera att ett föremål i vila påverkas av en uppåtriktad yttre kraft, den normala kraften kommer att vara mindre än objektets vikt.
Exempel: Normalkraften är 25, 15 N
Metod 5 av 5: Normal kraft och friktion

Steg 1. Känn den grundläggande ekvationen för kinetisk friktion
Kinetisk friktion, eller friktion för ett rörligt objekt, är lika med friktionskoefficienten gånger den normala kraften hos ett objekt. I ekvationsform: f = * N
- I denna ekvation, f symboliserar friktion, ️ representerar friktionskoefficienten och N representerar objektets normalkraft.
- "Friktionskoefficienten" är förhållandet mellan friktionskraften och normalkraften, som komprimerar två motstående ytor.
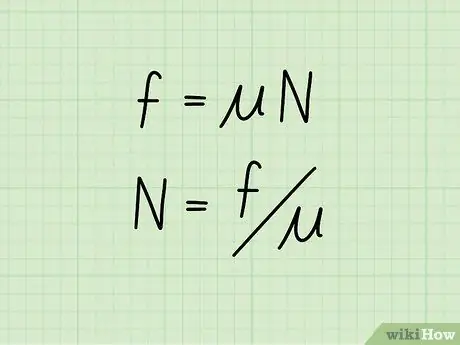
Steg 2. Sätt upp ekvationen för att isolera normalkraften
Om du känner till värdet på ett objekts kinetiska friktion, liksom dess friktionskoefficient, kan du beräkna normalkraften med hjälp av formeln: N = f /
- Båda sidorna av den ursprungliga ekvationen divideras med ️och därigenom isolera den normala kraften på ena sidan medan friktionskoefficienten och kinetisk friktion beräknas på den andra.
- Exempel: Hitta den normala kraften för ett block om friktionskoefficienten är 0,4 och storleken på den kinetiska friktionen är 40 N.
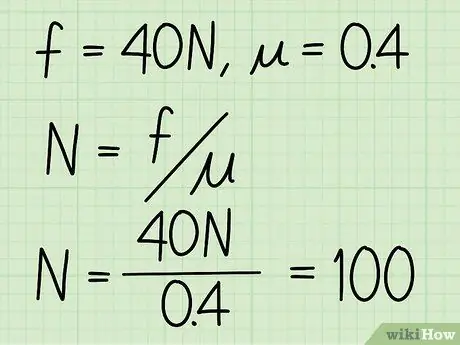
Steg 3. Dela den kinetiska friktionen med friktionskoefficienten
I grund och botten är detta allt du behöver göra för att hitta storleken på den normala kraften.
Exempel: N = f / = 40/0, 4 = 100
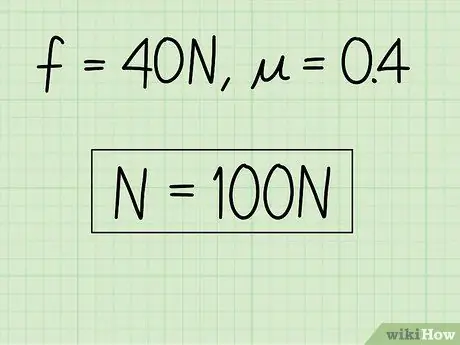
Steg 4. Skriv ner dina svar
Om så önskas kan du kontrollera ditt svar genom att ansluta det till den ursprungliga ekvationen för kinetisk friktion. Om du inte vill ha det har du löst problemet.






